Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 3
12 min
30
Question 1
Arthur participe à un concours de pêche, voici ce qu'il a péché : 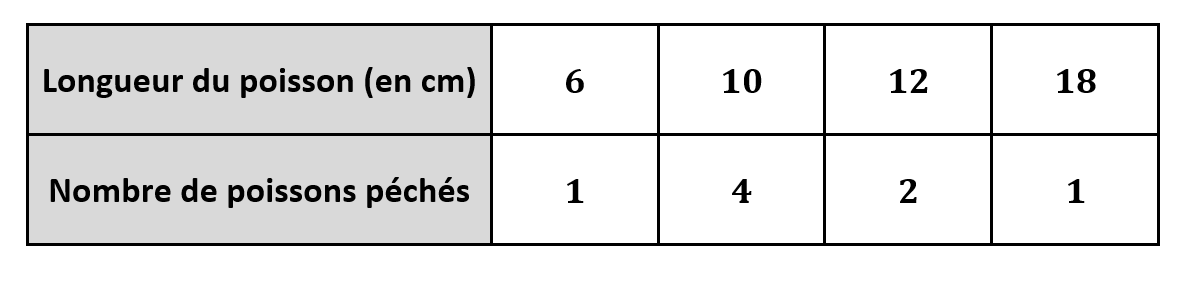

Combien de poissons Arthur a-t-il péché en tout
Correction
A l'aide du tableau ci-dessus on a :
Au total Arthur a péché poissons.
Au total Arthur a péché poissons.
Question 2
Quel est la taille moyenne des poissons péchés par Arthur
Correction
La moyenne d'une série statistique est le réel, noté , tel que :
Ici, correspond à l'effectif total ( le nombre total de poissons), c'est à dire : . Il vient alors que :
.
On peut donc conclure que la taille moyenne des poissons péchés est de cm.
Question 3
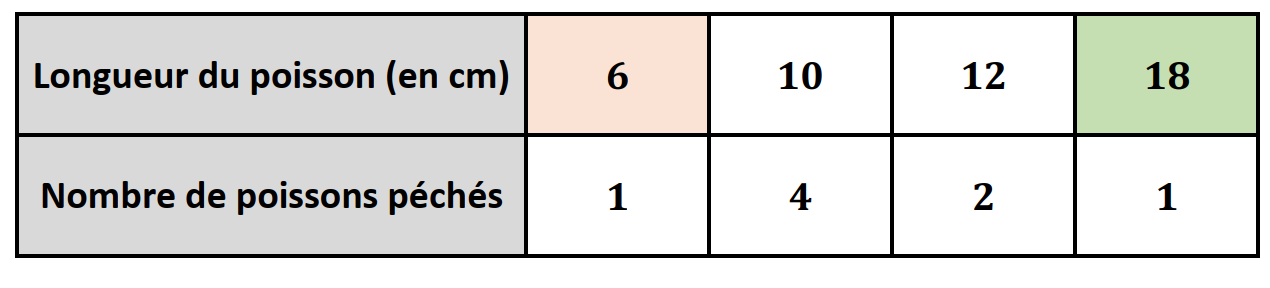
Quelle est l'étendue des tailles de poissons
Correction
L’étendue de cette série statistique est donc de .
Question 4
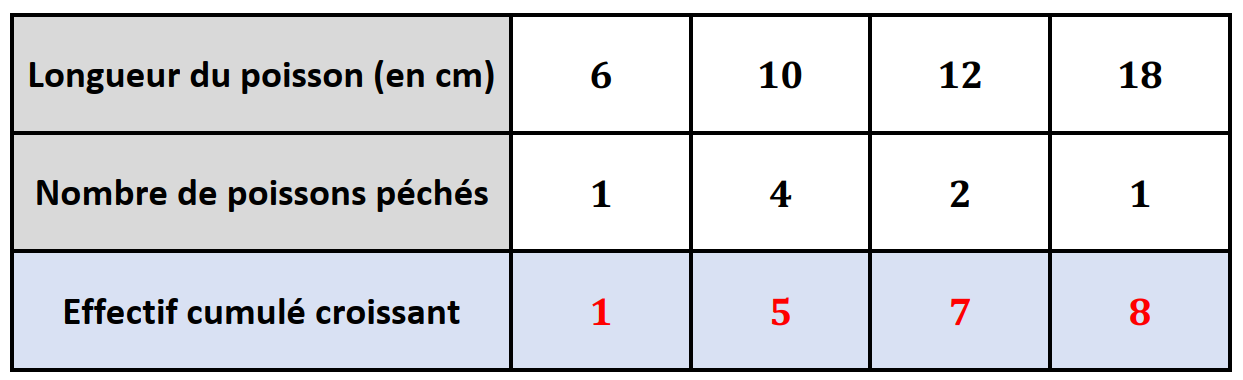
Quelle est la taille médiane des poissons péchés par Arthur Interpréter ce résultat
Correction
Nous partageons cette série statistique en deux groupes de même effectif. Comme l'effectif total est , nous pouvons créer deux groupes de valeurs.
La note médiane est comprise dans notre tableau entre la et la valeur .
( Elles appartiennent toutes les deux à la même catégorie : cm.)
On peut donc conclure que la taille médiane des poissons est
Question 5
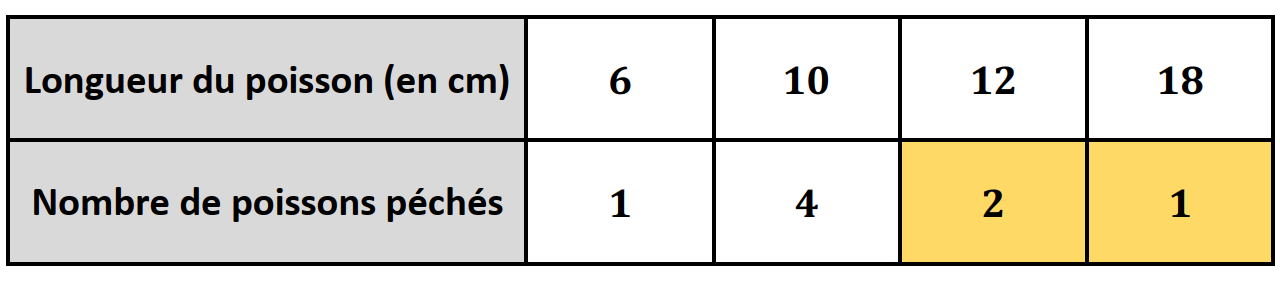
Quel pourcentage de poissons péchés par Arthur mesure cm ou plus Arrondir à l'unité.
Correction
- Calculer un pourcentage c'est donner une proportion sous forme d'une fraction.
La fraction doit être de dénominateur 100. - Pour calculer la proportion d’un nombre A par rapport à un nombre total B :
- On utilise la formule suivante
On peut donc conclure que des poissons péchés mesure cm ou plus.( le résultat est arrondi à l'unité près).
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.