Proportionnalité

Calculer la quatrième proportionnelle - Exercice 1

6 min
10
COMPETENCE : Reconnaître des situations de proportionnalité et résoudre les problèmes correspondants.
Question 1
Dans chaque cas, calculer la quatrième proportionnelle.

Compléter le tableau de proportionnalité suivant :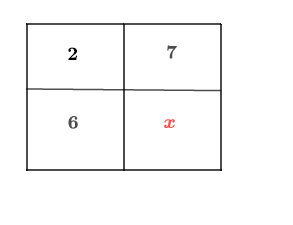

Correction
    Dans un tableau de proportionnalité, les produits en croix obtenus avec deux colonnes sont égaux.
    Si : ab=cd  \bf\color{red}\frac{a}{b}=\frac{c}{d}\; alors à l'aide du produit on croix on peut sortir l'égalité suivante : a×d=b×c.  \bf\color{red}a\times{d}=b\times{c}.\; En effet :
Ici on a un tableau de proportionnalité , par conséquent :
2×x=7×6  ⇒2\times{x}=7\times6\;\Rightarrow Ici on utilise le produit en croix.
2x=422x=42
x=422x=\frac{42}{2}
x=21\boxed{x=21}
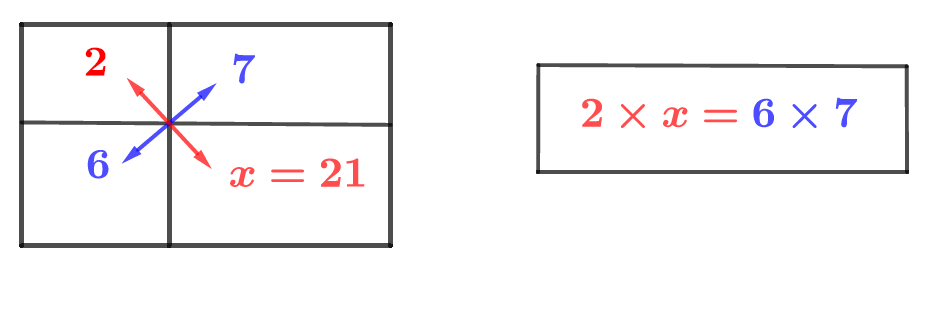
Question 2

Compléter le tableau de proportionnalité suivant :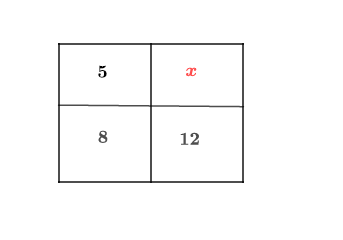

Correction
  • Dans un tableau de proportionnalité, les produits en croix obtenus avec deux colonnes sont égaux.
    Si : ab=cd  \bf\color{red}\frac{a}{b}=\frac{c}{d}\; alors à l'aide du produit on croix on peut sortir l'égalité suivante : a×d=b×c.  \bf\color{red}a\times{d}=b\times{c}.\; En effet :
Ici on a un tableau de proportionnalité , par conséquent :
8×x=5×12  ⇒8\times{x}=5\times12\;\Rightarrow Ici on utilise le produit en croix.
8x=608x=60
x=608x=\frac{60}{8}
x=7,5\boxed{x=7,5}
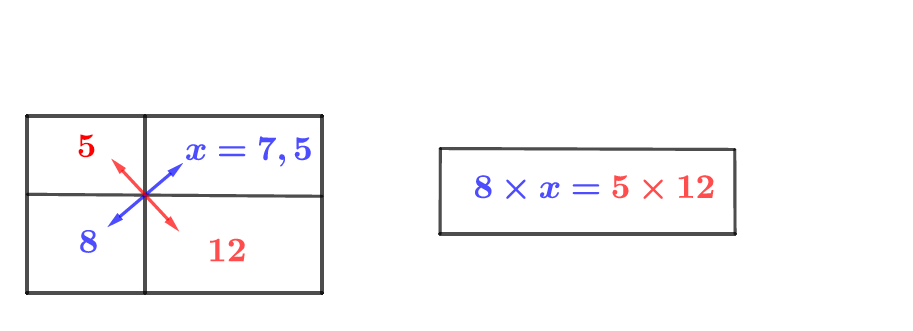
Question 3

Compléter le tableau de proportionnalité suivant :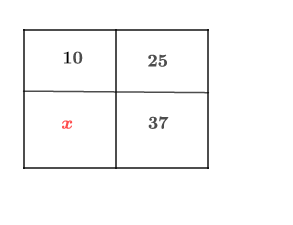

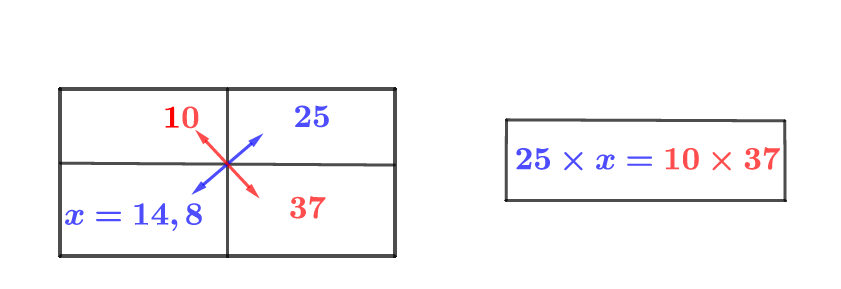
Correction
  • Dans un tableau de proportionnalité, les produits en croix obtenus avec deux colonnes sont égaux.
    Si : ab=cd  \bf\color{red}\frac{a}{b}=\frac{c}{d}\; alors à l'aide du produit on croix on peut sortir l'égalité suivante : a×d=b×c.  \bf\color{red}a\times{d}=b\times{c}.\; En effet :
Ici on a un tableau de proportionnalité , par conséquent :
25×x=10×37  ⇒25\times{x}=10\times37\;\Rightarrow Ici on utilise le produit en croix.
25x=37025x=370
x=37025x=\frac{370}{25}
x=14,8\boxed{x=14,8}
Question 4

Compléter le tableau de proportionnalité suivant :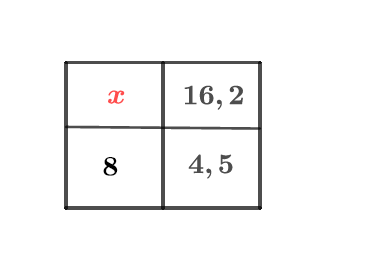

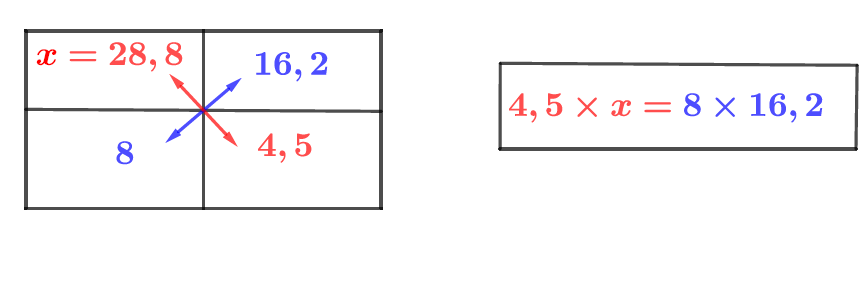
Correction
  • Dans un tableau de proportionnalité, les produits en croix obtenus avec deux colonnes sont égaux.
    Si : ab=cd  \bf\color{red}\frac{a}{b}=\frac{c}{d}\; alors à l'aide du produit on croix on peut sortir l'égalité suivante : a×d=b×c.  \bf\color{red}a\times{d}=b\times{c}.\; En effet :
Ici on a un tableau de proportionnalité , par conséquent :
4,5×x=8×16,2  ⇒4,5\times{x}=8\times16,2\;\Rightarrow Ici on utilise le produit en croix.
4,5x=129,64,5x=129,6
x=129,64,5x=\frac{129,6}{4,5}
x=28,8\boxed{x=28,8}
Question 5

Compléter le tableau de proportionnalité suivant :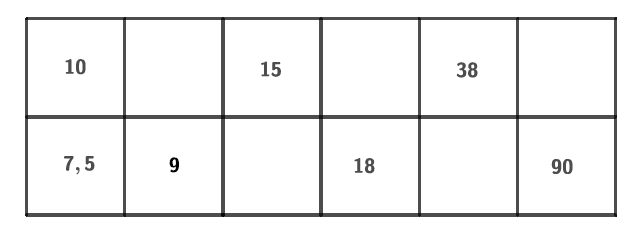

Correction
Ici on pourrait utiliser le produit en croix en utilisant à chaque fois deux colonnes pour compléter notre tableau.
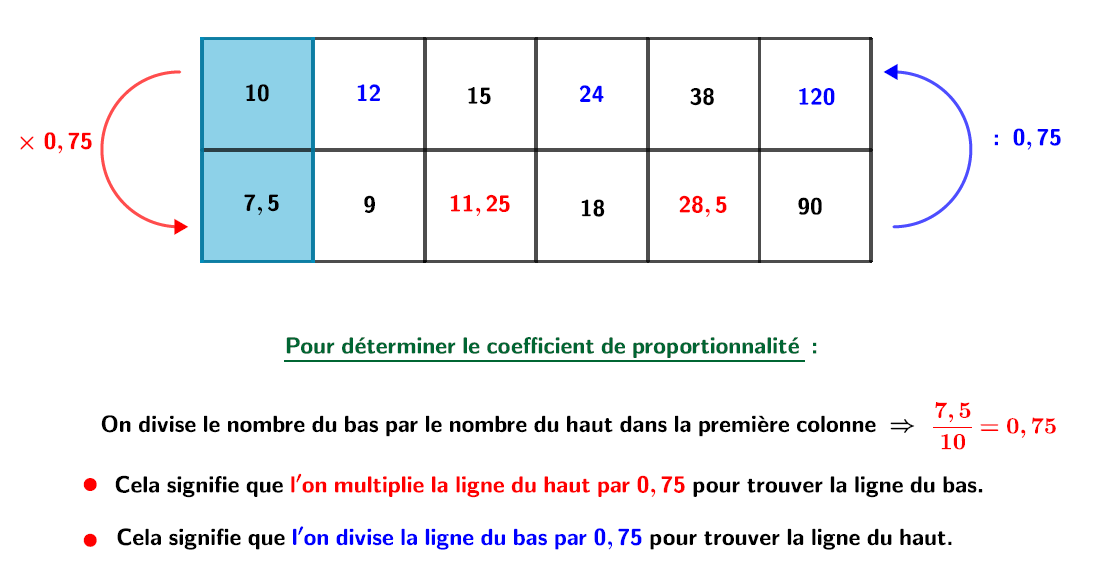
Cependant, dans un tableau de plusieurs colonnes, il est plus judicieux de travailler avec le coefficient de proportionnalité (vu en 5ème), pour compléter notre tableau.
    Pour obtenir le coefficient de proportionnalité on peut au choix :
  • Soit diviser le nombre du bas par celui du haut dans la même colonne.
  • Ou diviser le nombre du haut par celui du bas dans la même colonne.