Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 1ère partie - Exercice 1

18 min
35
Question 1
On considère un jeu composé d’un plateau tournant et d’une boule. Représenté ci-contre, ce plateau comporte 1313 cases numérotées de 00 à 1212. On lance la boule sur le plateau, la boule finit par s’arrêter au hasard sur une case numérotée. La boule a la même probabilité de s’arrêter sur chaque case.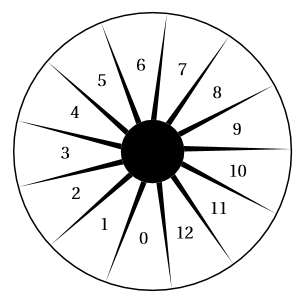

Quelle est la probabilité que la boule s'arrête sur la case numérotée 88?

Correction
Il y a une seule case numérotée 88 sur 1313 cases possibles.
Donc la probabilité que la boule s'arrête sur la case numérotée 88 est : 113\blue{\boxed{\frac{1}{13}}}
Question 2

Quelle est la probabilité que le numéro de la case sur lequel la boule s'arrête soit un nombre impair?

Correction
Il y a 66 cases numérotée par un nombre impair : 1;3,5,7,9,11{1;3,5,7,9,11}
On a 1313 cases possibles, la probabilité est donc égale à 613\blue{\boxed{\frac{6}{13}}}
Question 3

Quelle est la probabilité que le numéro de la case sur laquelle la boule s'arrête soit un nombre premier?

Correction
  • Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs.
  • Ces deux diviseurs sont 1 et le nombre lui-même.

    • Les nombres premiers sont donc : 2,3,5,7,11{2,3,5,7,11}
    Il y a 55 cases numérotées par un nombre premier sur 1313 cases possibles, la probabilité est donc égale à 513\blue{\boxed{\frac{5}{13}}}
    Question 4

    Lors des deux derniers lancers, la boule s’est arrêtée à chaque fois sur la case numérotée 99.  \; A-t-on maintenant plus de chances que la boule s’arrête sur la case numérotée 99 plutôt que sur la case numérotée 77?  \; Argumenter à l’aide d’un calcul de probabilité.

    Correction
    À chaque lancer la probabilité que la boule s’arrête sur une case est la même, égale à 113\blue{\boxed{\frac{1}{13}}}.
    La probabilité que la boule s’arrête sur la case numérotée 99 est donc égale à la probabilité que la boule s’arrête sur la case numérotée 77.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.