Fonction affine
Exercices types : partie 2 - Exercice 1
10 min
15
Question 1
Un cinéma propose trois tarifs :
Tarif « Classique » : La personne paye chaque entrée euros.
Tarif « Essentiel » : La personne paye un abonnement annuel de euros, puis chaque entrée coûte euros.
Tarif « Liberté » : La personne paye un abonnement annuel de euros avec un nombre d’entrées illimité.
Tarif « Classique » : La personne paye chaque entrée euros.
Tarif « Essentiel » : La personne paye un abonnement annuel de euros, puis chaque entrée coûte euros.
Tarif « Liberté » : La personne paye un abonnement annuel de euros avec un nombre d’entrées illimité.
Avec le tarif « Classique », une personne souhaite acheter trois entrées au cinéma.
Combien va-t-elle payer ?
Combien va-t-elle payer ?
Correction
Tarif « Classique » : La personne paye chaque entrée euros.
Une personne souhaite achetée trois entrées, elle paiera donc :
Une personne souhaite achetée trois entrées, elle paiera donc :
Question 2
Avec le tarif « Essentiel », une personne souhaite aller huit fois au cinéma.
Montrer qu’elle va payer euros.
Montrer qu’elle va payer euros.
Correction
Tarif « Essentiel » : La personne paye un abonnement annuel de euros, puis chaque entrée coûte euros.
Après l'abonnement annuel de euros, chaque place est à euros, on a donc :
Après l'abonnement annuel de euros, chaque place est à euros, on a donc :
Question 3
Dans la suite, x désigne le nombre d’entrées au cinéma.
On considère les trois fonctions f , g et h suivantes :
On considère les trois fonctions f , g et h suivantes :
Associer, sans justifier, chacune de ces fonctions au tarif correspondant.
Correction
Tarif « Classique » : La personne paye chaque entrée euros.
Cela correspond donc à la fonction :
Tarif « Essentiel » : La personne paye un abonnement annuel de euros, puis chaque entrée coûte euros.
Cela correspond donc à la fonction :
Tarif « Liberté » : La personne paye un abonnement annuel de euros avec un nombre d’entrées illimité.
Cela correspond donc à la fonction :
En effet, ici, qu'importe le nombre d'entrées, le prix reste le même, c'est-à-dire euros.
Cela correspond donc à la fonction :
Tarif « Essentiel » : La personne paye un abonnement annuel de euros, puis chaque entrée coûte euros.
Cela correspond donc à la fonction :
Tarif « Liberté » : La personne paye un abonnement annuel de euros avec un nombre d’entrées illimité.
Cela correspond donc à la fonction :
En effet, ici, qu'importe le nombre d'entrées, le prix reste le même, c'est-à-dire euros.
Question 4
Le graphique ci-dessous représente le prix à payer en fonction du nombre d’entrées pour chacun de ces trois tarifs.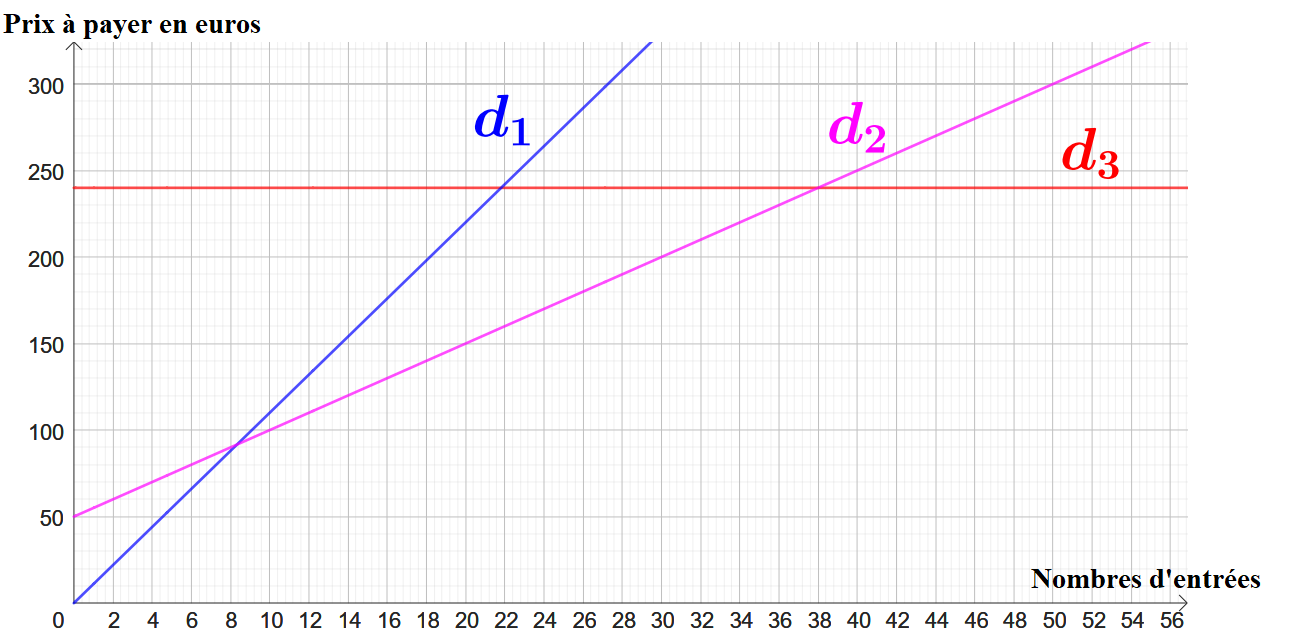
La droite représente la fonction correspondant au tarif « Classique ».
La droite représente la fonction correspondant au tarif « Essentiel ».
La droite représente la fonction correspondant au tarif « Liberté ».

La droite représente la fonction correspondant au tarif « Classique ».
La droite représente la fonction correspondant au tarif « Essentiel ».
La droite représente la fonction correspondant au tarif « Liberté ».
Quel tarif propose un prix proportionnel au nombre d’entrées ?
Correction
- Graphiquement, une situation de proportionnalité est représentée par une droite qui passe par l'origine du repère
le tarif « Classique », qui propose un prix proportionnel au nombre d’entrées.
Question 5
Pour les questions suivantes, aucune justification n’est attendue.
Avec euros, combien peut-on acheter d’entrées au maximum avec le tarif « Essentiel»
Correction
Ici, on souhaite déterminer l'antécédent de par la fonction , pour cela :
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
Graphiquement, on peut conclure qu'avec euros, on peut acheter au maximum entrées avec le tarif « Essentiel».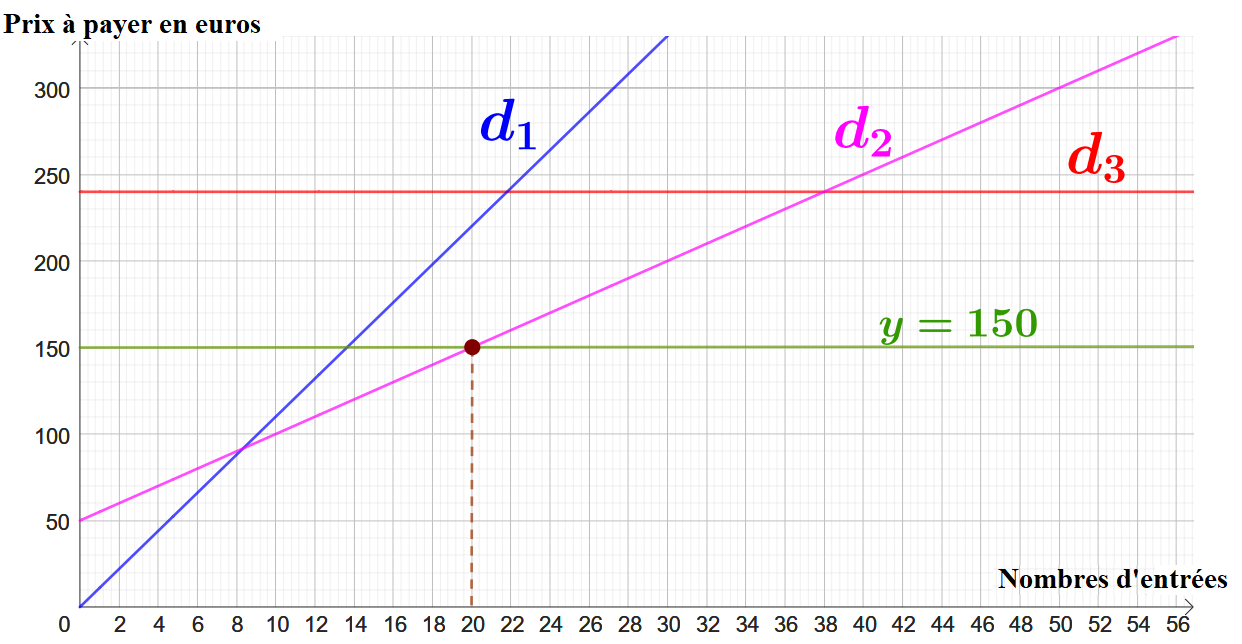
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
Graphiquement, on peut conclure qu'avec euros, on peut acheter au maximum entrées avec le tarif « Essentiel».

Question 6
À partir de combien d’entrées, Tarif « Liberté » devient-il le tarif le plus intéressant
Correction
Graphiquement, on peut conclure qu'à partir de entrées le tarif « Liberté» devient le plus intéressant.
En effet, à partir de ce point-là, la droite se situe en dessous la droite et .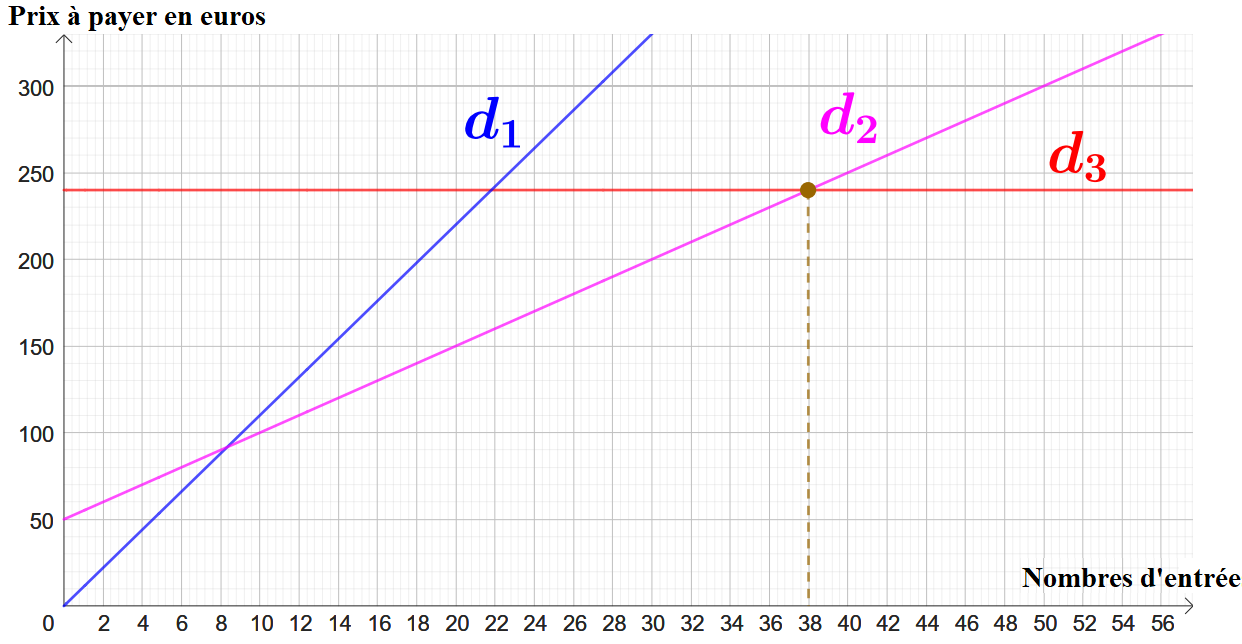
En effet, à partir de ce point-là, la droite se situe en dessous la droite et .

Question 7
Si on décide de ne pas dépasser un budget de euros, quel est le tarif qui permet d’acheter le plus grand nombre d’entrées ?
Correction
Ici, on souhaite déterminer la dernière droite que coupe la droite d'équation , pour cela :
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
Graphiquement, on peut conclure que si on ne veut pas dépasser un budget de euros, c'est le tarif « Essentiel» que l'on doit choisir. (La droite ).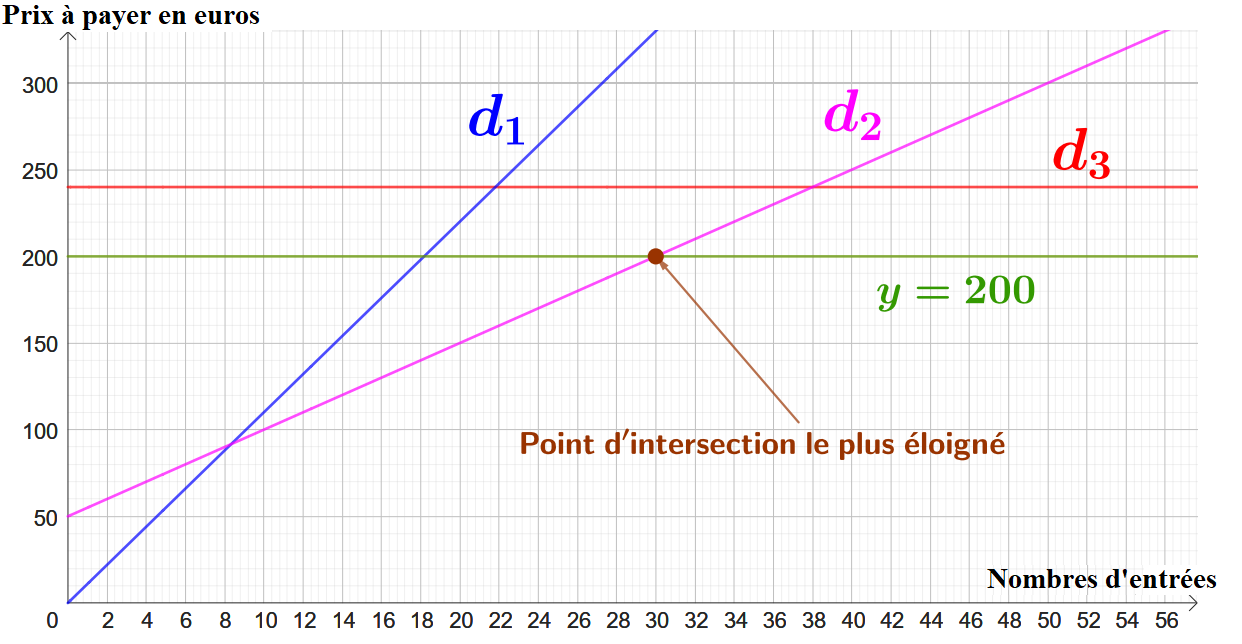
On repère le point d'ordonnée , et ensuite, on rejoint la courbe horizontalement. (Cela revient à tracer la droite d'équation .)
Ensuite, au(x) point(s) d'intersection de la droite d'équation et de la courbe, on rejoint l'axe des abscisses. (En ce point se trouve là où les valeur(s) recherchée(s).)
Graphiquement, on peut conclure que si on ne veut pas dépasser un budget de euros, c'est le tarif « Essentiel» que l'on doit choisir. (La droite ).
