Fonction affine
Exercices types : partie 1 - Exercice 1
25 min
45
Question 1
Pour le paiement de la garderie dans une école, on propose deux formules :
Formule A : on paie pour devenir adhérent pour l’année scolaire puis on paye par mois
de garderie.
Formule B : pour les non-adhérents, on paye par mois.
de garderie.
Pour chacune des formules, calculer le prix payé pour mois de garderie.
Correction
Avec la formule A :
On paie pour devenir adhérent pour l’année scolaire puis on paye par mois. Soit :
Avec la formule B :
On paye par mois Soit :
On paie pour devenir adhérent pour l’année scolaire puis on paye par mois. Soit :
Avec la formule B :
On paye par mois Soit :
Question 2
On appelle le nombre de mois de garderie.
On note le prix payé avec la formule et le prix payé avec la formule
On note le prix payé avec la formule et le prix payé avec la formule
Exprimer puis en fonction de
Correction
Avec la formule A :
on paie pour devenir adhérent pour l’année scolaire puis on paye par mois.
Soit le nombre de mois de garderie. On a donc :
Avec la formule B :
On paye par mois.
Soit le nombre de mois de garderie. On a donc :
on paie pour devenir adhérent pour l’année scolaire puis on paye par mois.
Soit le nombre de mois de garderie. On a donc :
Avec la formule B :
On paye par mois.
Soit le nombre de mois de garderie. On a donc :
Question 3
Représenter graphiquement les fonctions suivantes dans un même repère :
et
On prendra 1 cm pour 1 mois en abscisse.
On prendra 1 cm pour 10 € en ordonnée.
et
Correction
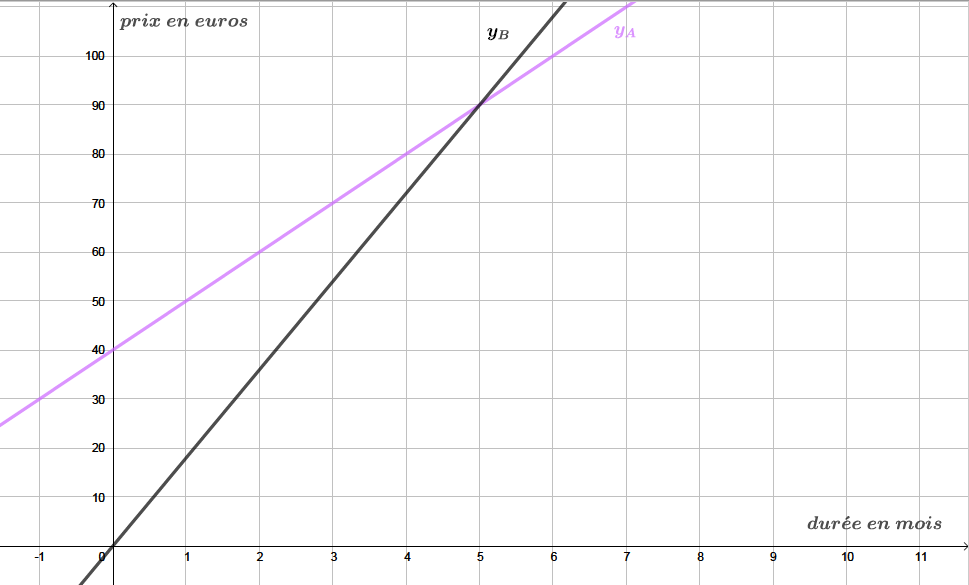
Question 4
A partir du graphique, déterminer le nombre de mois pour lequel les prix à payer sont les mêmes.
Correction
Le nombre de mois pour lequel les prix à payer sont les mêmes correspond au point intersection des deux droites et . 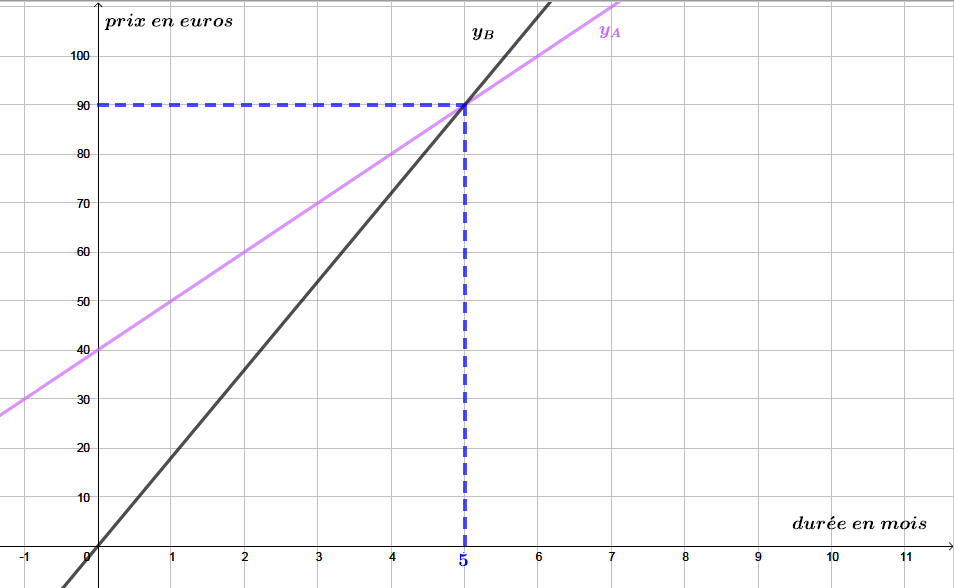 On peut donc conclure que pour mois d'abonnement, le prix à payer est le même.
On peut donc conclure que pour mois d'abonnement, le prix à payer est le même.

Question 5
Retrouver le résultat précédent par le calcul.
Correction
Le prix à payer est identique, lorsque :
Il faut donc résoudre l'équation :
. On soustrait à chaque membre.
. On soustrait à chaque membre.
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
L'ensemble des solutions est .
On trouve bien ici la même valeur que la question précédente.
Il faut donc résoudre l'équation :
- On doit dans un premier temps rassembler les termes en dans le membre de gauche.
. On soustrait à chaque membre.
. On soustrait à chaque membre.
. On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
L'ensemble des solutions est .
On trouve bien ici la même valeur que la question précédente.
Question 6
À partir du graphique, déterminer la formule la plus avantageuse si on ne paie que mois dans l’année.
Correction
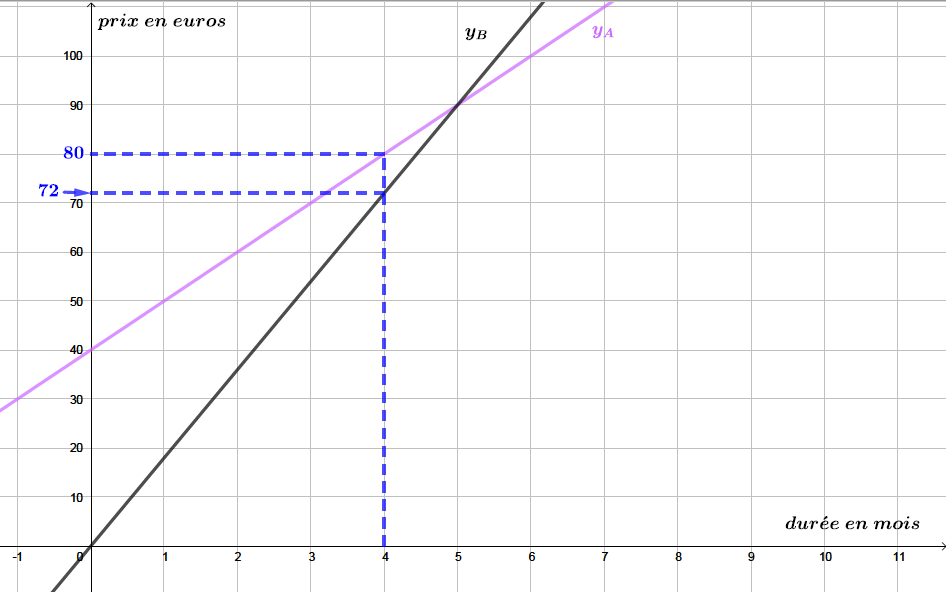
On peut donc conclure que pour mois d'abonnement, la formule est la plus avantageuse.
Question 7
On dispose d’un budget de Combien de mois de garderie au maximum pourra-t-on payer si l’on choisit la formule
Correction
La formule est définie par la fonction suivante :
Pour déterminer le nombre de mois que l'on peut payer avec un budget de , il nous faut résoudre l'équation suivante :
soit
équivaut successivement à :
On soustrait à chaque membre.
On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
Ici, on peut conclure qu'avec euros, on pourra payer au maximum mois plein.
Pour déterminer le nombre de mois que l'on peut payer avec un budget de , il nous faut résoudre l'équation suivante :
soit
équivaut successivement à :
On soustrait à chaque membre.
On divise chaque membre par le nombre devant le qui ici vaut .
Ainsi :
Ici, on peut conclure qu'avec euros, on pourra payer au maximum mois plein.