Équations et programme de calculs

Exercices types : partie 2 - Exercice 1

20 min
35
Question 1
Voici un programme de calcul :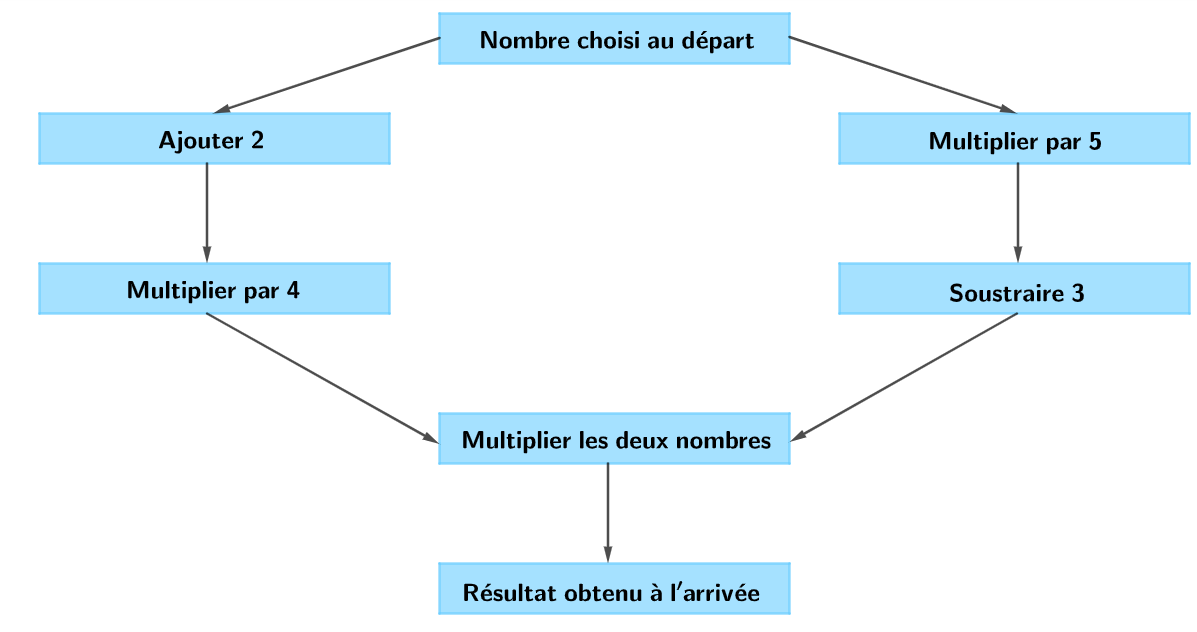

Montrer que si on choisit 22 comme nombre de départ, le résultat à l’arrivée est 112.112.

Correction
1°) Déterminons le résultat obtenu à gauche :
première étape :
Le nombre choisi est 2.\color{blue}2.
deuxième étape :
On additionne 22 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; 2+2=4.\color{blue}2+2=4.
troisième étape :
On multiplie 44 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; 4×4=16.\color{blue}4\times4=16.
2°) Déterminons le résultat obtenu à droite :
première étape :
Le nombre choisi est 2.\color{blue}2.
deuxième étape :
On multiplie par 55 ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; 5×2=10.\color{blue}5\times2=10.
troisième étape :
On soustrait 33 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; 10−3=7.\color{blue}10-3=7.
On multiplie le résultat trouvé à gauche avec celui de droite :
On obtient donc   \;⇒\color{red}\Rightarrow   \; 16×7=112.\color{blue}16\times7=112.
On peut donc conclure que si le nombre de départ est 22 le résultat du programme est 112112.
Question 2

Quel est le résultat obtenu à l’arrivée quand on choisit −3-3 comme nombre de départ ?

Correction
1°) Déterminons le résultat obtenu à gauche :
première étape :
Le nombre choisi est −3.\color{blue}-3.
deuxième étape :
On additionne 22 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; −3+2=−1.\color{blue}-3+2=-1.
troisième étape :
On multiplie 44 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; −1×4=−4.\color{blue}-1\times4=-4.
2°) Déterminons le résultat obtenu à droite :
première étape :
Le nombre choisi est −3.\color{blue}-3.
deuxième étape :
On multiplie par 55 ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; −3×5=−15.\color{blue}-3\times5=-15.
troisième étape :
On soustrait 33 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; −15−3=−18.\color{blue}-15-3=-18.
On multiplie le résultat trouvé à gauche avec celui de droite :
On obtient donc   \;⇒\color{red}\Rightarrow   \; −4×(−18)=72.\color{blue}-4\times(-18)=72.
On peut donc conclure que si le nombre de départ est −4-4 le résultat du programme est 7272.
Question 3
On choisit xx comme nombre de départ.

Parmi les expressions suivantes, lesquelles permettent d’exprimer le résultat à l’arrivée de ce programme de calcul.
Aucune justification n’est demandée.

Correction
1°) Déterminons le résultat obtenu à gauche :
première étape :
Le nombre choisi est x.\color{blue}x.
deuxième étape :
On additionne 22 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; x+2\color{blue}x+2
troisième étape :
On multiplie 44 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; 4(x+2).\color{blue}4(x+2).
2°) Déterminons le résultat obtenu à droite :
première étape :
Le nombre choisi est x.\color{blue}x.
deuxième étape :
On multiplie par 55 ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; x×5=5x.\color{blue}x\times5=5x.
troisième étape :
On soustrait 33 à ce nombre.
On obtient donc   \;⇒\color{red}\Rightarrow   \; 5x−3.\color{blue}5x-3.
On multiplie le résultat trouvé à gauche avec celui de droite :
On obtient donc   \;⇒\color{red}\Rightarrow   \; 4(x+2)(5x−3)=(4x+8)(5x−3).\color{blue}4(x+2)(5x-3)=(4x+8)(5x-3).
On peut donc conclure que l'expression CC et l'expression DD sont correctes.
Question 4

Trouver les deux nombres de départ qui permettent d’obtenir 00 à l’arrivée. Expliquer la démarche.

Correction
Ici il nous faut résoudre l'équation : (4x+8)(5x−3)=0(4x+8)(5x-3)=0
  • Le produit de 2 facteurs est nul si et seulement si l'un de ses facteurs est nul.
  • Résoudre une équation produit revient à résoudre deux équations du premier degré.
(4x+8)(5x−3)=0{\left(4x+8\right)\left(5x-3\right)=0}       \;\;\;Si et seulement si :         \;\;\;\;4x+8=04x+8 = 0          \;\;\;\;\; ou :          \;\;\;\;\; 5x−3=05x-3 =0
Ainsi, on a :
4x+8=04x+8=0
4x+8−8=0−84x+8{\color{blue}{-8}} =0{\color{blue}{-8}}   \; On soustrait 8{\color{blue}8} à chaque membre.
4x=−84x =-8
4x4=−84\frac{4x}{\color{blue}{4}} =\frac{-8}{\color{blue}{4}} On divise par 4{\color{blue}4} chaque membre.
x=−2\boxed{x=-2}
                                                                            \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; OU\textbf{\red{OU}}
5x−3=05x-3=0
5x−3+3=0+35x-3{\color{blue}{+3}} =0{\color{blue}{+3}}   \; On additionne 3{\color{blue}3} à chaque membre.
5x=35x =3
5x5=35\frac{5x}{\color{blue}{5}} =\frac{3}{\color{blue}{5}} On divise par 5{\color{blue}5} chaque membre.
x=35\boxed{x=\frac{3}{5}}
En choisissant −2-2 et 35\frac{3}{5} comme nombre de départ, on obtiendra 00 à l'arrivée.
Question 5

Développer et réduire l’expression B.B.

Correction
  • Méthode pour développer une expression.
    Définition : Développer une expression, c'est la transformer en somme.
    • 1°) Développement d'un nombre par une somme : Si on considère 4 nombres relatifs, (a,  b,  c,  d)(a,\;b,\;c,\;d),  \;
    alors : (a+b)(c+d)=a×c+a×d+b×c+b×d{\color{red}\boxed{(a+b)(c+d)=a\times{c}+a\times{d}+b\times{c}+b\times{d}}}
B=(4x+2)(5x−3)B=(4x+2)(5x-3)
B=4x×5x+4x×(−3)+2×5x+2×(−3)\small{B=4x\times{5x}+4x\times{(-3)}+2\times{5x}+2\times{(-3)}}
B=20x2−12x+10x−6\small{B=20x^2-12x+10x-6}
B=20x2−2x−6\color{blue}\boxed{B=20x^2-2x-6}