Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

QCM - Exercice 1

12 min
25
Question 1
Une espèce d’oiseaux rares voit sa population diminuer de 3%3\% chaque année. On recense 300300 oiseaux de cette espèce en 20172017. On modélise le nombre d’oiseaux de cette espèce en l’année 2017+n2017+n par une suite (un)\left(u_{n}\right). Ainsi u0=300u_{0} = 300.

En 20182018, la population sera de :
  • 291291 oiseaux
  • 297297 oiseaux
  • 309309 oiseaux
  • 210210 oiseaux

Correction
La bonne réponse est aa.
Chaque année, la population diminue de 3%3\%.
On multiplie donc chaque année la population par le coefficient multiplicateur q=1−3100=0,97q=1-\frac{3}{100}=0,97 .
Il en résulte donc que : u1=u0×0,97=300×0,97u_{1}=u_{0}\times0,97=300\times0,97
D'où :
u1=291u_{1}=291
Question 2

La suite (un)\left(u_{n}\right) est :
  • arithmétique de raison −9-9
  • géométrique de raison 0,030,03
  • géométrique de raison 1,031,03
  • géométrique de raison 0,970,97

Correction
La bonne réponse est dd.
Chaque année, la population diminue de 3%3\%.
On multiplie donc chaque année la population par le coefficient multiplicateur q=1−3100=0,97q=1-\frac{3}{100}=0,97 . Chaque terme se déduit du précédent en le multipliant par 0,970,97 .
Il en résulte donc que la suite (vn)\left(v_{n}\right) est geˊomeˊtrique{\color{blue}\text{géométrique}} de raison q=0,97q=0,97
Question 3
On donne la feuille de tableur ci-dessous :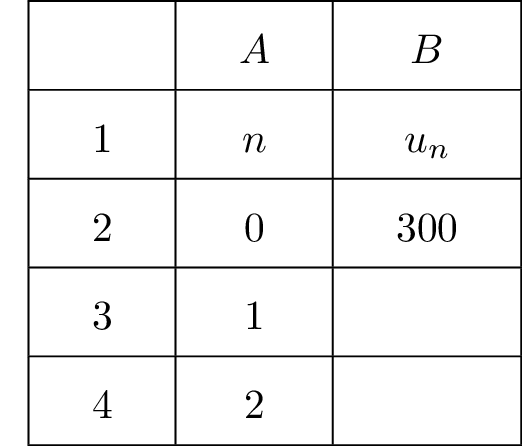

Quelle formule saisie dans la cellule B3 permettra d’afficher les termes successifs de la suite (un)\left(u_{n}\right) en l’étirant vers le bas?
  • ==B2−0,03-0,03
  • ==B2∗0,03*0,03
  • ==B2∗0,97*0,97^A2
  • ==B2∗0,97*0,97

Correction
La bonne réponse est dd.
D'après la question précédente, nous savons que chaque terme se déduit du précédent en le multipliant par 0,970,97 .
Or, ici la population est modélisée par la colonne B.
Il en résulte donc qu'il faut choisir l'expression ==B2∗0,97*0,97
Question 4
On donne un extrait des résultats obtenus dans la feuille de tableur précédente :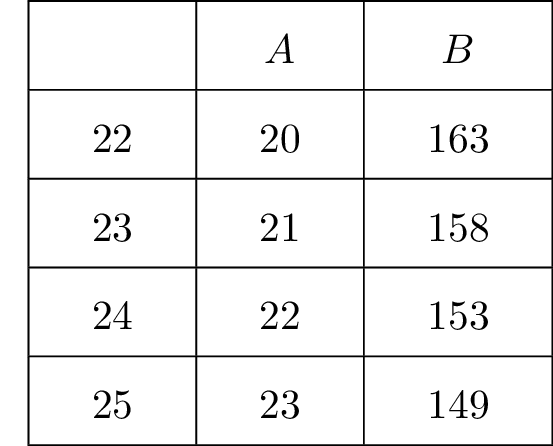

On peut en déduire que la population aura diminué de moitié par rapport à 20172017 à partir de :
  • 20392039
  • 20402040
  • 20412041
  • 20422042

Correction
La bonne réponse est bb.
La colonne A correspond à l'indice nn. Au départ, nous avions u0=300u_{0} = 300 oiseaux dans la population en 20172017.
Puis pour n=23n=23, nous avons 149149 oiseaux . La population aura donc diminué de moitié pour l'année 2017+23=20402017+{\color{blue}23}=2040.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.