Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Sujet 1 - Exercice 1

40 min
65
Partie  A  :Etude  d’une  fonction\bf{Partie\;A\;: Etude\;d’une\;fonction}
Question 1
Soit ff la fonction définie sur R\mathbb{R} par f(x)=0,005x(x+56).f(x) = 0,005x(x + 56).

Quelle est la nature de la courbe représentative de ff ?

Correction
f(x)=0,005x(x+56).f(x) = 0,005x(x + 56). On peut égale"ment écrire f(x)f(x) sous la forme :
f(x)=0,005(x+0)(x+56)\color{blue}f(x)=0,005(x+0)(x+56)
  • Or La représentation graphique de la fonction x↦a(x−x1)(x−x2)x\mapsto a\left(x-x_1\right)\left(x-x_2\right) où aa, x1x_1 et x2x_2 sont des constantes réelles avec a≠0a\ne 0 est une parabole.
On  peut  donc  conclure  que  la  courbe  repreˊsentative  de  f  est  une  parabole.\color{black}On\;peut\;donc\;conclure\;que\;la\;courbe\;représentative\;de\;f\;est\;une\;\color{red}parabole.
Question 2

Représenter l’allure de la courbe représentative de f.f.

Correction
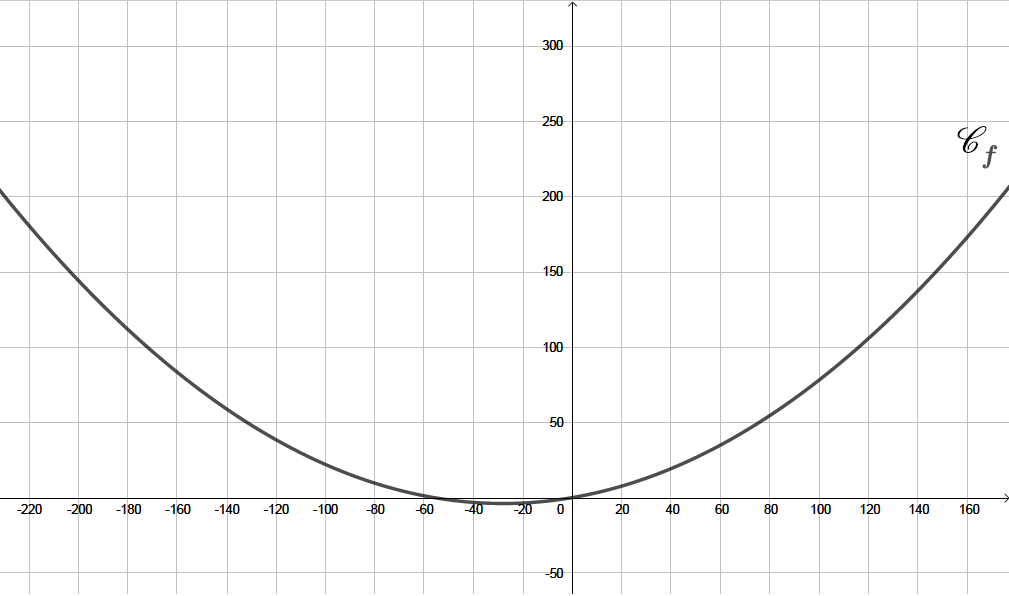
Question 3

Déterminer les points d'intersection de la courbe C\mathscr{C} et de l'axe des abscisses.

Correction
1°)  les  abscisses  des  points  d’intersection  de  Cf  avec  l’axe  des  abscisses‾\color{blue}\underline{1°)\;les\;abscisses\;des\;points\;d’intersection\;de\;\mathscr{C_f}\;avec\;l’axe\;des\;abscisses}
Pour déterminer l’intersection de la courbe de ff avec l’axe des abscisses, il suffit de résoudre l’équation f(x)=0f\left(x\right)=0 .
Ainsi :
f(x)=0,005(x+0)(x+56)f\left(x\right)=0,005(x+0)\left(x+56\right) . Il s'agit ici d'une équation produit nul.
Il faut donc résoudre : x+0=0x+0=0 ou\text{\red{ou}} x+56=0x+56=0
D’une part :\text{\blue{D'une part :}}
x+0=0x+0=0
x=0x=0
D’autre part :\text{\blue{D'autre part :}}
x+56=0x+56=0
x=−56x=-56
Les points cherchés ont pour coordonnées (0  ;  0,005)\left(0\;;\;0,005\right) et (0  ;  −56)\left(0\;;\;-56\right)
Question 4

Déterminer une équation de l'axe de symétrie de la parabole C\mathscr{C} .

Correction
  • La représentation graphique de la fonction x↦a(x−x1)(x−x2)x\mapsto a\left(x-x_1\right)\left(x-x_2\right) où aa, x1x_1 et x2x_2 sont des constantes réelles avec a≠0a\ne 0 est une parabole ayant la droite x=x1+x22x=\frac{x_1+x_2}{2} comme axe de symétrie.
Nous avons f(x)=0,005(x+0)(x+56)f\left(x\right)=0,005(x+0)\left(x+56\right) . D'après le rappel, nous pouvons identifier que x1=0x_1=0 et x2=−56x_2=-56 .
L'axe de symétrie admet comme équation x=x1+x22x=\frac{x_1+x_2}{2}, il vient alors :
x=0+−562x=\frac{0+-56}{2}
x=−562x=-\frac{56}{2}
x=−28x=-28

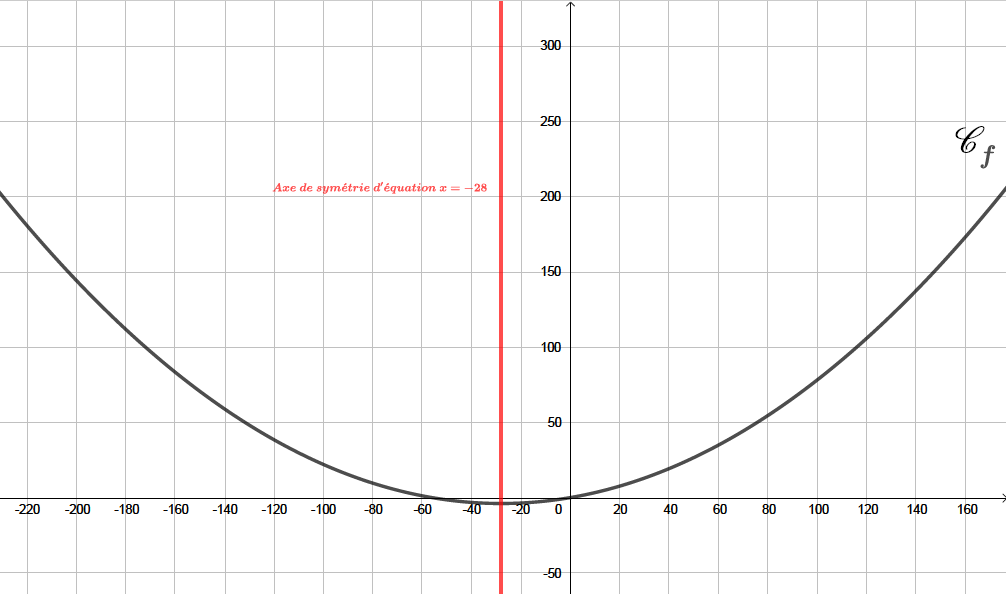
Question 5
On s’intéresse dans la suite de cet exercice à la distance d’arrêt en mètres d’un vehicule sur route humide, puis sur route sèche, en fonction de sa vitesse en km/h.km/h.
Partie  B  :Sur  route  humide\bf{Partie\;B\;: Sur\;route\;humide}
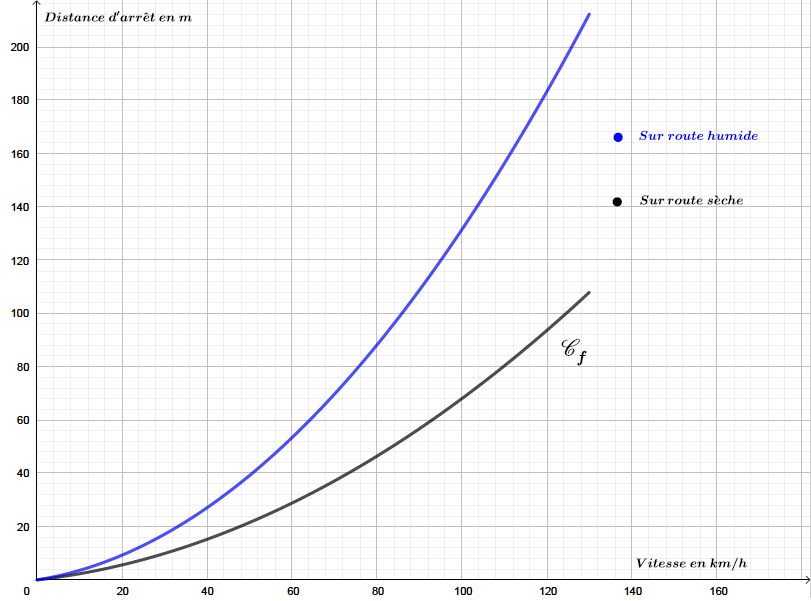
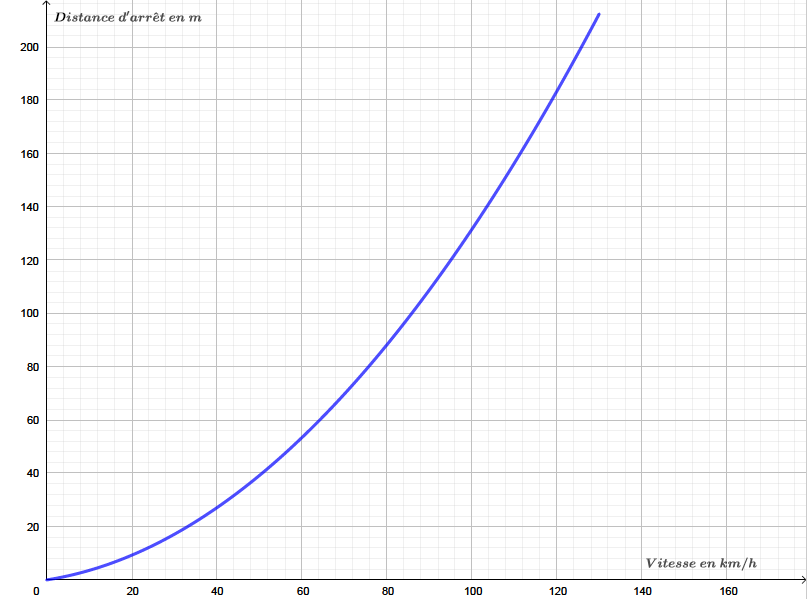
Le graphique fourni ci dessous, représente la distance d’arrêt en mètres d’un véhicule sur route humide en fonction de la vitesse en km/h.km/h.
En s’aidant du graphique ci-dessus, et en faisant apparaître les traits utiles à la lecture, déterminer avec la précision que permet la lecture graphique :

La distance d'arrêt en mètres d’un véhicule automobile roulant à une vitesse de 80  km/h80\;km/h puis à une vitesse de 90  km/h90\;km/h

Correction
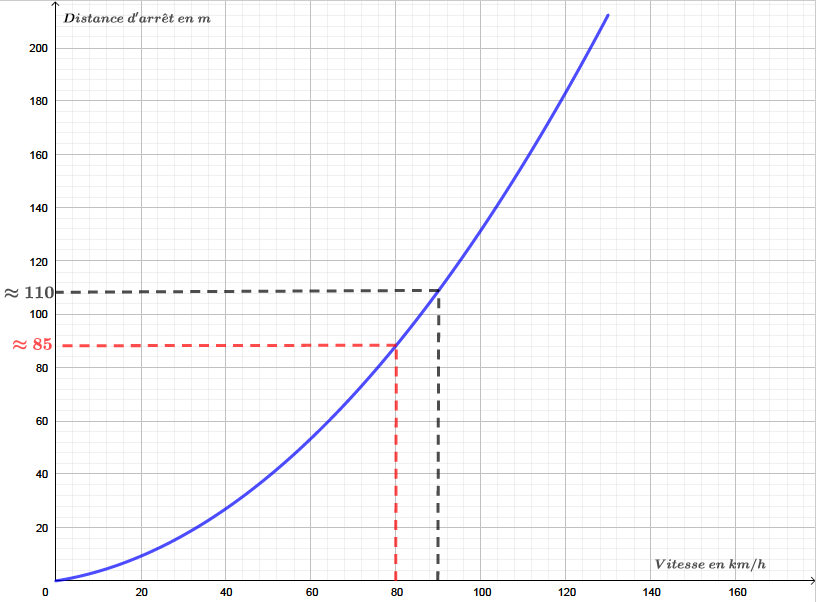
  • A L'aide du graphique, on constate que la distance d'arrêt d’un véhicule automobile roulant à une vitesse de 80  km/h80\;km/h est de 85  meˋtres  environ.\color{red}85\;mètres\;environ.
  • A L'aide du graphique, on constate que la distance d'arrêt d’un véhicule automobile roulant à une vitesse de 80  km/h80\;km/h est de 110  meˋtres  environ.\color{red}110\;mètres\;environ.

    • Question 6

    La vitesse en km/hkm/h correspondant à une distance d’arrêt de 6060 mètres.

    Correction
  • A L'aide du graphique, on constate que la vitesse correspondant à une distance d'arrêt de 60 mètres est de la 65  km/h.\color{red}65\;km/h.
    • Question 7
    Partie  C  :  Sur  route  seˋche\bf{Partie\;C\;:\;Sur\;route\;sèche}
    Sur route sèche, la distance d’arrêt en mètres d’un véhicule roulant à x  km/hx\;km/h est modélisée par la fonction ff de la partie AA définie uniquement sur [0;130][0; 130] par f(x)=0,005x(x+56).f(x) = 0,005x(x + 56).

    Calculer f(80).f(80). Interpréter ce résultat dans le contexte de l’exercice.

    Correction
    Nous avons f(x)=0,005(x+0)(x+56)f\left(x\right)=0,005(x+0)\left(x+56\right) .
    f(80)=0,005(80+0)(80+56)f(80)=0,005(80+0)(80+56)
    f(80)=0,005×80×136f(80)=0,005\times80\times136
    f(80)=54\color{blue}\boxed{f(80)=54}
    De ce résultat, on peut en déduire que la distance d'arrêt d'un véhicule roulant à 80  km/h80\;km/h sur route sèche est de 5454 mètres.
    Question 8

    Compléter le tableau de valeurs de la fonction ff ci-dessous. Arrondir les valeurs à l’unité.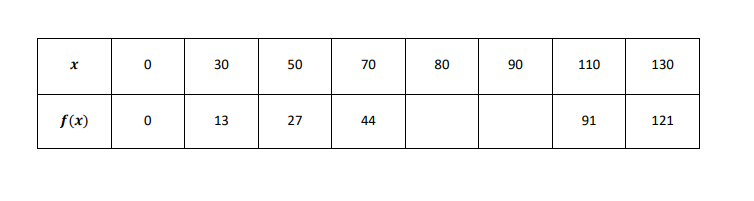

    Correction
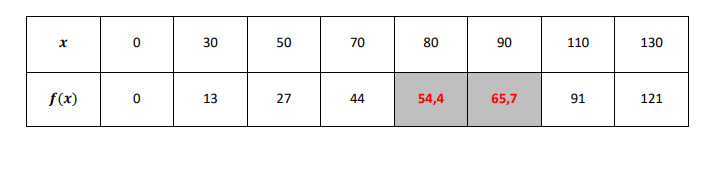
    Question 9

    Tracer la courbe représentative Cf\mathscr{C_f} de la fonction ff sur l’intervalle [0;130].[0 ; 130].

    Correction
    Question 10
    Partie  D:\bf{Partie\;D} :
    Une campagne publicitaire de la Sécurité Routière du mois de juin 20182018 affirme que baisser la vitesse sur les routes de 90  km/h90\;km/h à 80  km/h80\;km/h permet de gagner 1313 mètres au moment du freinage.
    En utilisant les résultats des parties BB et C  :C\;:

    Peut-on dire que cette affirmation est vérifiée sur route humide ? Justifier la réponse.

    Correction
  • A L'aide du graphique de la question 5, on a constaté que la distance d'arrêt d’un véhicule automobile roulant à une vitesse de 80  km/h80\;km/h est de 85  meˋtres  environ  sur  route  humide.\color{red}85\;mètres\;environ \;sur\;route\;humide.
  • A L'aide du graphique de la question 5, on a constaté que la distance d'arrêt d’un véhicule automobile roulant à une vitesse de 80  km/h80\;km/h est de 110  meˋtres  environ  sur  route  humide.\color{red}110\;mètres\;environ \;sur\;route\;humide.
    Donc la distance gagné est environ égale à : 110−85=15  meˋtres\color{red}\boxed{110-85=15\;mètres}
    On  peut  donc  en  deˊduire  que  l’affirmation  de  la  campagne  publicitaire  est  vraie.\color{black}On\;peut\;donc\;en\;déduire\;que\;l’affirmation\;de\;la\;campagne\;publicitaire\;est\;vraie.
    • Question 11

    Peut-on dire que cette affirmation est vérifiée sur route sèche ? Justifier la réponse.

    Correction
    A l'aide du tableau de la question 88^(Le tableau) on constate :
  • Que la distance d'arrêt à 80  km/h80\;km/h est de 54,4  m.54,4\;m.
  • Que la distance d'arrêt à 900  km/h900\;km/h est de 65,7  m.65,7\;m.
    Donc la distance gagné est égale à : 65,7−54,4=11,3  meˋtres\color{red}\boxed{65,7-54,4=11,3\;mètres}
    On  peut  donc  en  deˊduire  que  l’affirmation  de  la  campagne  publicitaire  n′est  pas  vraie.\color{black}On\;peut\;donc\;en\;déduire\;que\;l’affirmation\;de\;la\;campagne\;publicitaire\;n'est\;pas\;vraie.

    • Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.