Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Produit scalaire : définition analytique . Mise en situation - Exercice 1

10 min
25
Question 1
Dire dans chacun des cas suivants si le triangle ABCABC est rectangle ou non .

A(−1;4)A\left(-1;4\right) , B(9;6)B\left(9;6\right) et C(4;0)C\left(4;0\right)

Correction
  • Dans un repère orthonormé (0;i→;j→)\left(0;\overrightarrow{i} ;\overrightarrow{j}\right) , le produit scalaire de deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} de coordonnées respectives (x;y)\left(x;y\right) et (x′;y′)\left(x';y'\right) est égal à :
    u→⋅v→=xx′+yy′\overrightarrow{u} \cdot\overrightarrow{v}=xx'+yy'
Il va falloir commencer par placer les trois points dans un repère afin d'effectuer une conjecture que nous allons ensuite démontrer.
D'après la figure, si le triangle était rectangle il le serait en CC.
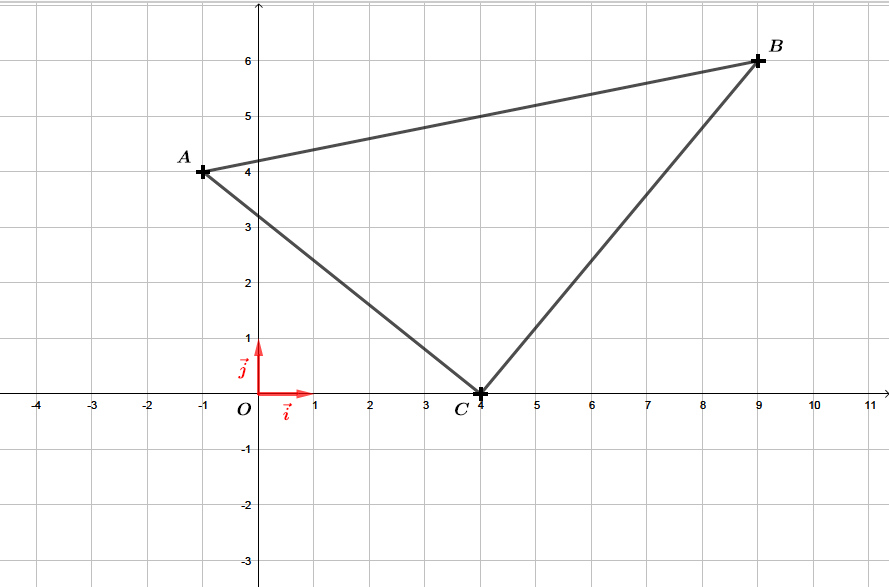
Pour le démontrer, il va falloir calculer les vecteurs CA→\overrightarrow{CA} et CB→\overrightarrow{CB} puis calculer le produit scalaire CA→⋅CB→\overrightarrow{CA} \cdot \overrightarrow{CB}
Premieˋrement :\blue{\text{Premièrement :}}
CA→(xA−xCyA−yC)\overrightarrow{CA} \left(\begin{array}{c} {x_{A} -x_{C} } \\ {y_{A} -y_{C} } \end{array}\right)
CA→(−1−44−0)\overrightarrow{CA} \left(\begin{array}{c} {-1-4} \\ {4-0} \end{array}\right)
CA→(−54)\overrightarrow{CA} \left(\begin{array}{c} {-5} \\ {4} \end{array}\right)
Deuxieˋmement :\blue{\text{Deuxièmement :}}
CB→(xB−xCyB−yC)\overrightarrow{CB} \left(\begin{array}{c} {x_{B} -x_{C} } \\ {y_{B} -y_{C} } \end{array}\right)
CB→(9−46−0)\overrightarrow{CB} \left(\begin{array}{c} {9-4} \\ {6-0} \end{array}\right)
CB→(56)\overrightarrow{CB} \left(\begin{array}{c} {5} \\ {6} \end{array}\right)
Finalement :\blue{\text{Finalement :}}
CA→⋅CB→=−5×5+4×6\overrightarrow{CA} \cdot \overrightarrow{CB} =-5\times5+4\times6
CA→⋅CB→=−25+24\overrightarrow{CA} \cdot \overrightarrow{CB} =-25+24
CA→⋅CB→=−1≠0\overrightarrow{CA} \cdot \overrightarrow{CB} =-1\ne0

Il en résulte que les vecteurs CA→\overrightarrow{CA} et CB→\overrightarrow{CB} ne sont pas orthogonaux.
Le triangle ABCABC n'est donc pas rectangle.
Deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} sont orthogonaux si et seulement u→⋅v→=0\overrightarrow{u} \cdot \overrightarrow{v} =0
Question 2

A(6;0)A\left(6;0\right) , B(0;2)B\left(0;2\right) et C(−4;−10)C\left(-4;-10\right)

Correction
  • Dans un repère orthonormé (0;i→;j→)\left(0;\overrightarrow{i} ;\overrightarrow{j}\right) , le produit scalaire de deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} de coordonnées respectives (x;y)\left(x;y\right) et (x′;y′)\left(x';y'\right) est égal à :
    u→⋅v→=xx′+yy′\overrightarrow{u} \cdot\overrightarrow{v}=xx'+yy'
Il va falloir commencer par placer les trois points dans un repère afin d'effectuer une conjecture que nous allons ensuite démontrer.
D'après la figure, si le triangle était rectangle il le serait en BB.
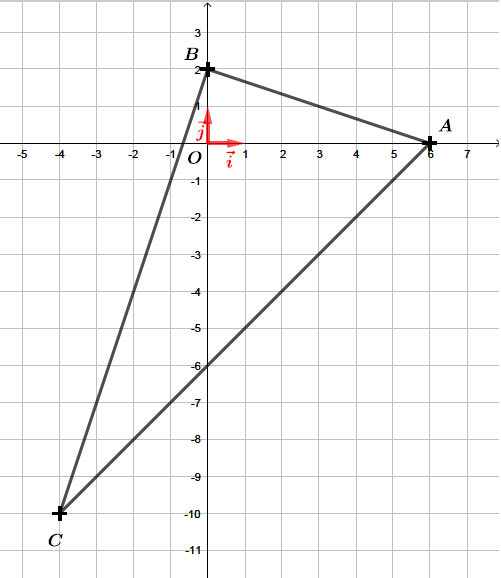
Pour le démontrer, il va falloir calculer les vecteurs BA→\overrightarrow{BA} et BC→\overrightarrow{BC} puis calculer le produit scalaire BA→⋅BC→\overrightarrow{BA} \cdot \overrightarrow{BC}
Premieˋrement :\blue{\text{Premièrement :}}
BA→(xA−xByA−yB)\overrightarrow{BA} \left(\begin{array}{c} {x_{A} -x_{B} } \\ {y_{A} -y_{B} } \end{array}\right)
BA→(6−00−2)\overrightarrow{BA} \left(\begin{array}{c} {6-0} \\ {0-2} \end{array}\right)
BA→(6−2)\overrightarrow{BA} \left(\begin{array}{c} {6} \\ {-2} \end{array}\right)
Deuxieˋmement :\blue{\text{Deuxièmement :}}
BC→(xC−xByC−yB)\overrightarrow{BC} \left(\begin{array}{c} {x_{C} -x_{B} } \\ {y_{C} -y_{B} } \end{array}\right)
BC→(−4−0−10−2)\overrightarrow{BC} \left(\begin{array}{c} {-4-0} \\ {-10-2} \end{array}\right)
BC→(−4−12)\overrightarrow{BC} \left(\begin{array}{c} {-4} \\ {-12} \end{array}\right)
Finalement :\blue{\text{Finalement :}}
BA→⋅BC→=6×(−4)+(−2)×(−12)\overrightarrow{BA} \cdot \overrightarrow{BC} =6\times\left(-4\right)+\left(-2\right)\times\left(-12\right)
BA→⋅BC→=−24+24\overrightarrow{BA} \cdot \overrightarrow{BC} =-24+24
BA→⋅BC→=0\overrightarrow{BA} \cdot \overrightarrow{BC} =0

Il en résulte que les vecteurs BA→\overrightarrow{BA} et BC→\overrightarrow{BC} sont orthogonaux.
Le triangle ABCABC est donc bien un triangle rectangle en BB .
Deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} sont orthogonaux si et seulement u→⋅v→=0\overrightarrow{u} \cdot \overrightarrow{v} =0
Question 3

A(0;3,5)A\left(0;3,5\right) , B(1;6)B\left(1;6\right) et C(6;4)C\left(6;4\right)

Correction
  • Dans un repère orthonormé (0;i→;j→)\left(0;\overrightarrow{i} ;\overrightarrow{j}\right) , le produit scalaire de deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} de coordonnées respectives (x;y)\left(x;y\right) et (x′;y′)\left(x';y'\right) est égal à :
    u→⋅v→=xx′+yy′\overrightarrow{u} \cdot\overrightarrow{v}=xx'+yy'
Il va falloir commencer par placer les trois points dans un repère afin d'effectuer une conjecture que nous allons ensuite démontrer.
D'après la figure, si le triangle était rectangle il le serait en BB.
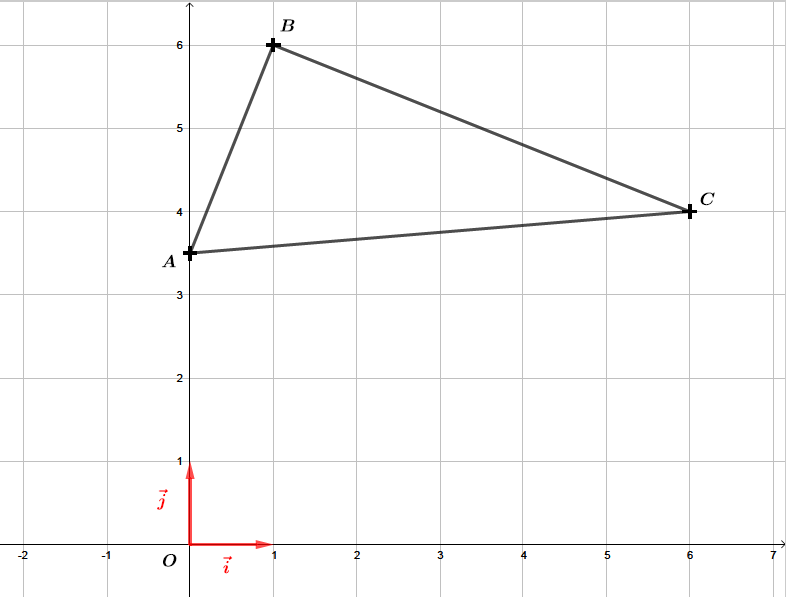
Pour le démontrer, il va falloir calculer les vecteurs BA→\overrightarrow{BA} et BC→\overrightarrow{BC} puis calculer le produit scalaire BA→⋅BC→\overrightarrow{BA} \cdot \overrightarrow{BC}
Premieˋrement :\blue{\text{Premièrement :}}
BA→(xA−xByA−yB)\overrightarrow{BA} \left(\begin{array}{c} {x_{A} -x_{B} } \\ {y_{A} -y_{B} } \end{array}\right)
BA→(0−13,5−6)\overrightarrow{BA} \left(\begin{array}{c} {0-1} \\ {3,5-6} \end{array}\right)
BA→(−1−2,5)\overrightarrow{BA} \left(\begin{array}{c} {-1} \\ {-2,5} \end{array}\right)
Deuxieˋmement :\blue{\text{Deuxièmement :}}
BC→(xC−xByC−yB)\overrightarrow{BC} \left(\begin{array}{c} {x_{C} -x_{B} } \\ {y_{C} -y_{B} } \end{array}\right)
BC→(6−14−6)\overrightarrow{BC} \left(\begin{array}{c} {6-1} \\ {4-6} \end{array}\right)
BC→(5−2)\overrightarrow{BC} \left(\begin{array}{c} {5} \\ {-2} \end{array}\right)
Finalement :\blue{\text{Finalement :}}
BA→⋅BC→=−1×5+(−2,5)×(−2)\overrightarrow{BA} \cdot \overrightarrow{BC}=-1\times5+\left(-2,5\right)\times\left(-2\right)
BA→⋅BC→=−5+5\overrightarrow{BA} \cdot \overrightarrow{BC} =-5+5
BA→⋅BC→=0\overrightarrow{BA} \cdot \overrightarrow{BC} =0

Il en résulte que les vecteurs BA→\overrightarrow{BA} et BC→\overrightarrow{BC} sont orthogonaux.
Le triangle ABCABC est donc bien un triangle rectangle en BB .
Deux vecteurs u→\overrightarrow{u} et v→\overrightarrow{v} sont orthogonaux si et seulement u→⋅v→=0\overrightarrow{u} \cdot \overrightarrow{v} =0