Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Sujet 1 - Exercice 1
12 min
30
Question 1
des élèves en première dans un lycée ont un Iphone. On constitue au hasard un échantillon de élèves de ce lycée. On suppose que le nombre d’élèves est suffisamment important pour que l’on puisse assimiler ce prélèvement à celui de trois tirages successifs avec remise. La variable aléatoire comptabilise le nombre d'élève ayant un IPhone dans l'échantillon.
Etablir l'arbre correspondant à la situation.
Correction
Son paramètre est la probabilité que l'élève possède un IPhone c'est à dire
Cela signifie que choisir un élève possédant un IPhone est une épreuve de Bernoulli.
On effectue trois tirages. On répète, donc, de façon épreuves de Bernoulli.
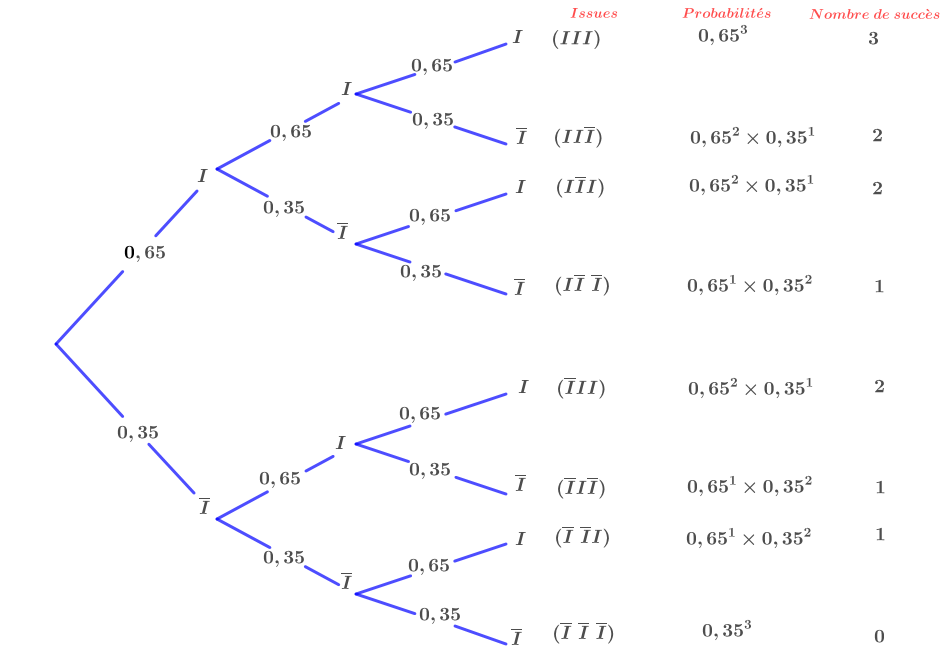
Question 2
Calculer et donner une valeur approchée à près .
Correction
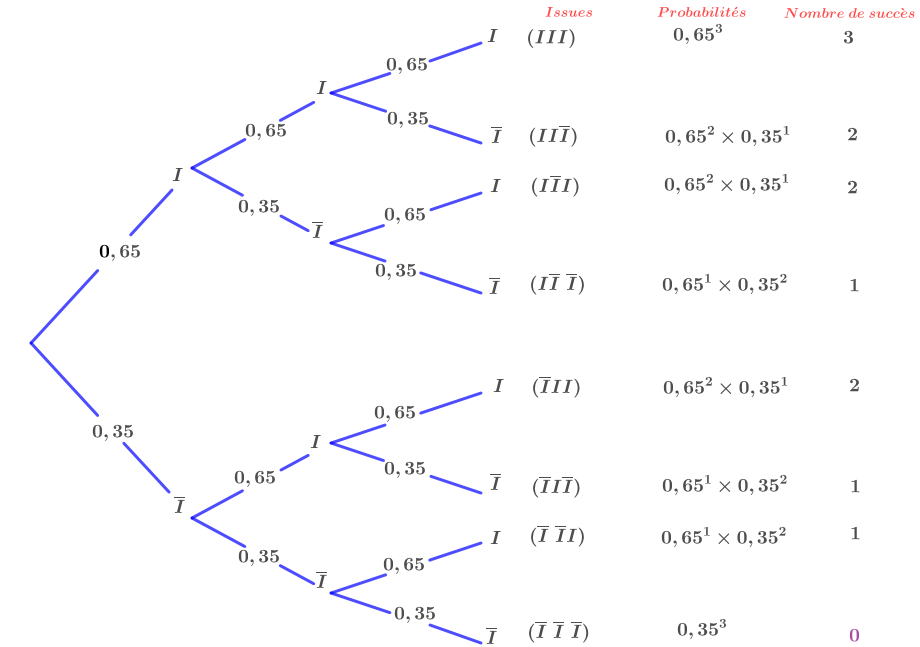
Ainsi :
D'où :
Question 3
Calculer et donner une valeur approchée à près .
Correction
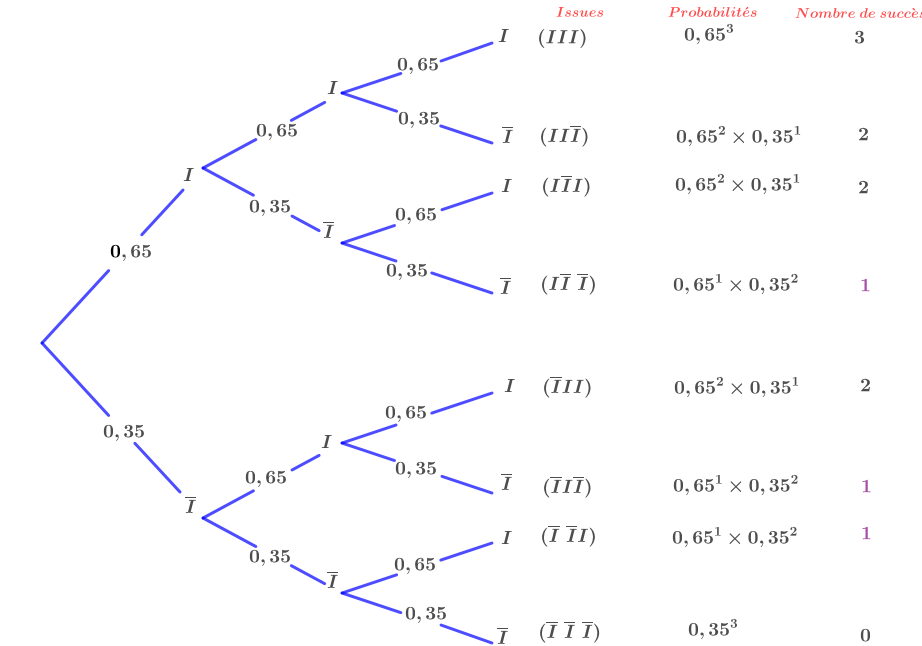
Ainsi :
D'où :
Question 4
Calculer et donner une valeur approchée à près .
Correction
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.