Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : 1ère partie - Exercice 2
20 min
35
Une entreprise, qui fabrique et vend des caméscopes numériques, modélise le bénéfice en euros pour caméscopes fabriquées et vendus en une journée, à l'aide de la fonction .
L'entreprise ne pouvant construire plus de caméscopes par jour. On aura ainsi :
L'entreprise ne pouvant construire plus de caméscopes par jour. On aura ainsi :
Question 1
Calculer le bénéfice pour puis pour caméscopes.
Correction
Il nous faut calculer et .
d'où d'où Le bénéfice pour caméscopes est de euros et pour caméscopes de euros
Question 2
Calculer où désigne la fonction dérivée de .
Correction
Question 3
Montrer que l'on peut écrire sous la forme .
Correction
Il nous suffit de développer l'expression : et montrer que cela nous donne bien
Il vient alors que :
équivaut successivement à :
Ainsi :
Il vient alors que :
équivaut successivement à :
Ainsi :
Question 4
Etudier le signe de sur l'intervalle .
Correction
Pour étudier le signe de , nous allons utiliser la forme .
Comme alors le signe de est du signe de .
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
On en déduit le tableau de signe de :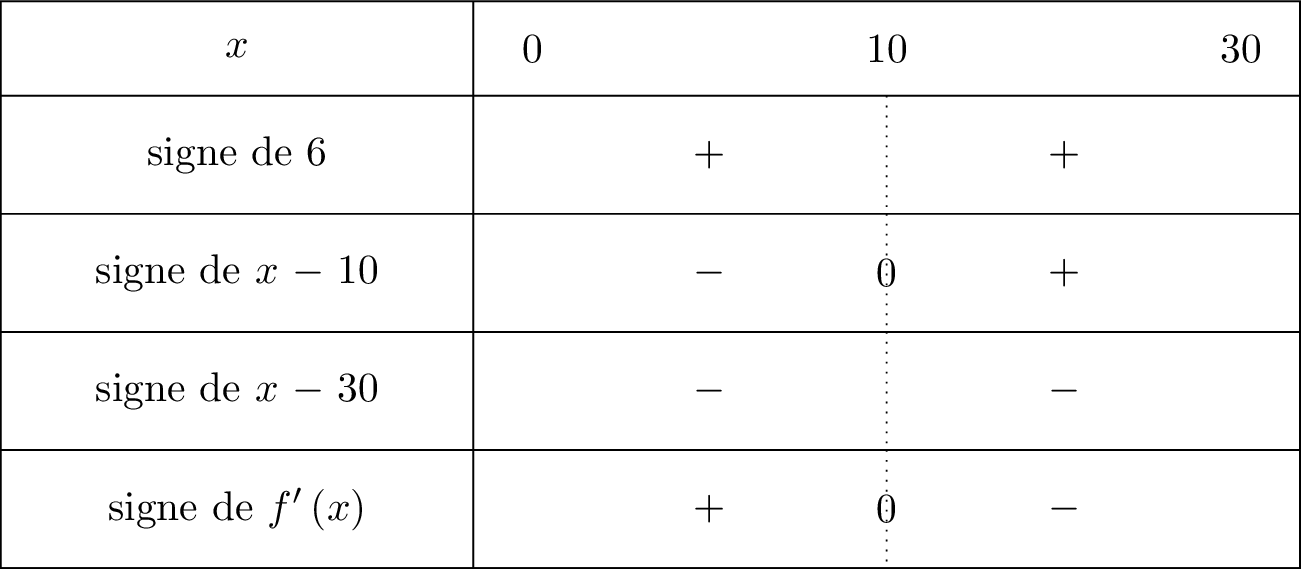
Comme alors le signe de est du signe de .
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
On en déduit le tableau de signe de :

Question 5
Dresser le tableau de variation de sur l'intervalle .
Correction
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .
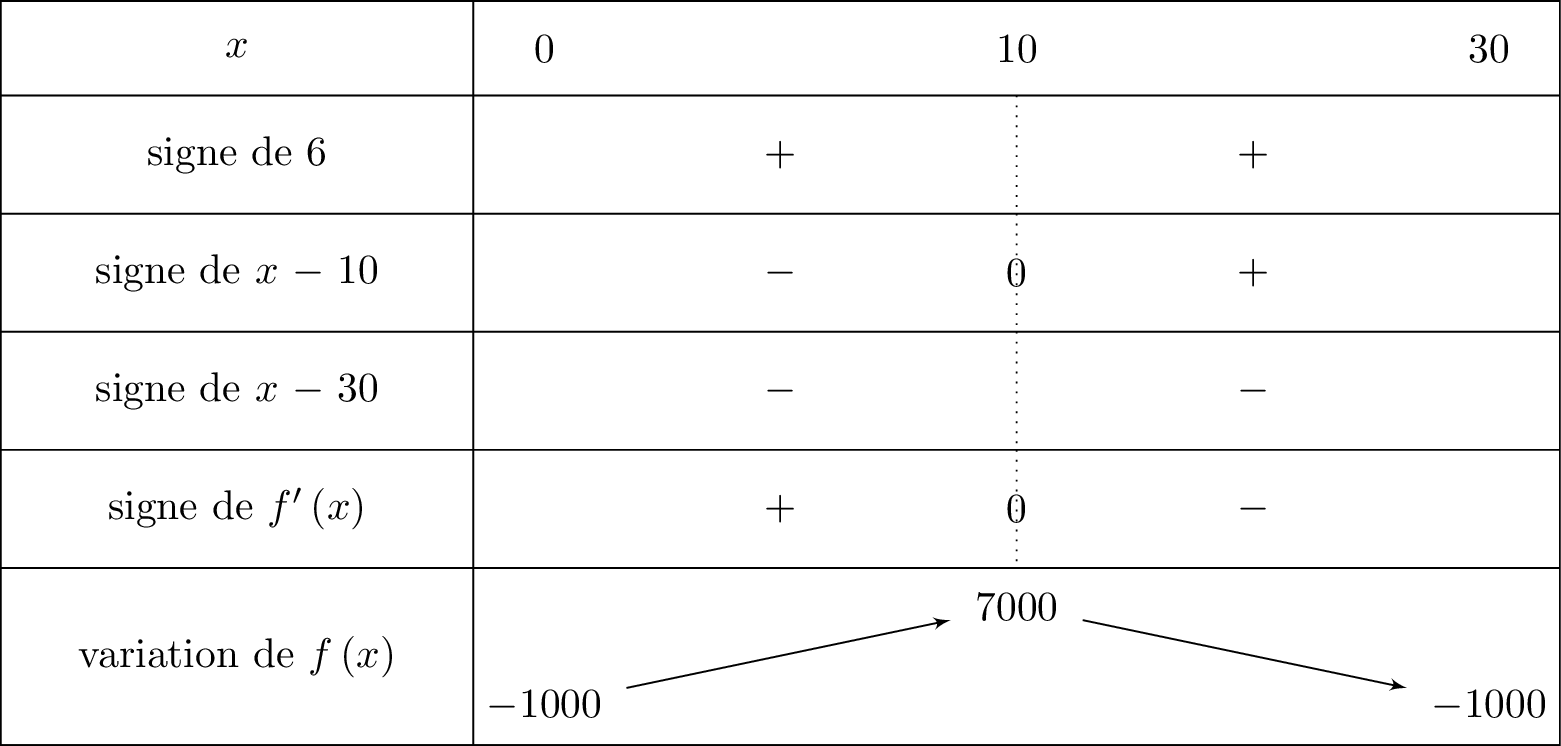
Question 6
En déduire combien de caméscopes l'entreprise doit fabriquer et vendre chaque jour pour avoir un bénéfice maximal. Donner ce bénéfice.
Correction
Pour avoir un bénéfice maximal, l'entreprise doit fabriquer et vendre chaque jour caméscopes. Le bénéfice sera de euros.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.