Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 1ère partie - Exercice 1

18 min
30
Une entreprise produit des panneaux solaires. Une étude de marché permet d’estimer que la production pour le mois à venir est comprise entre 15001500 et 30003000 panneaux solaires. On s’intéresse au bénéfice de l’entreprise sur la vente des panneaux solaires produits. On décide de modéliser l’évolution du bénéfice de l’entreprise, exprimé en centaine d’euros, par la fonction ff définie ci-dessous :
f(x)=−2x2+90x−400f\left(x\right)=-2x^{2}+90x-400
On admet que la fonction ff est dérivable sur l’intervalle [15;30]\left[15; 30\right] et on note f′f' sa fonction dérivée.
Question 1

Calculer la dérivée de ff notée f′f'.

Correction
  • La dérivée d'un nombre{\color{blue}nombre} est 0.{\color{blue}0} .
  • La dérivée d'un nombre×x{\color{blue}nombre\times x} est nombre.{\color{blue}nombre} .
  • La dérivée de x2{\color{blue}x^{2}} est 2x.{\color{blue}2x} .
  • La dérivée d'un nombre×x2{\color{blue}nombre\times x^{2}} est nombre×2x.{\color{blue}nombre\times2x} .

    • f(x)=−2x2+90x−400f\left(x\right)=-2x^{2}+90x-400
    f′(x)=−2×2x+90f'\left(x\right)=-2\times2x+90
    f′(x)=−4x+90f'\left(x\right)=-4x+90

    Question 2

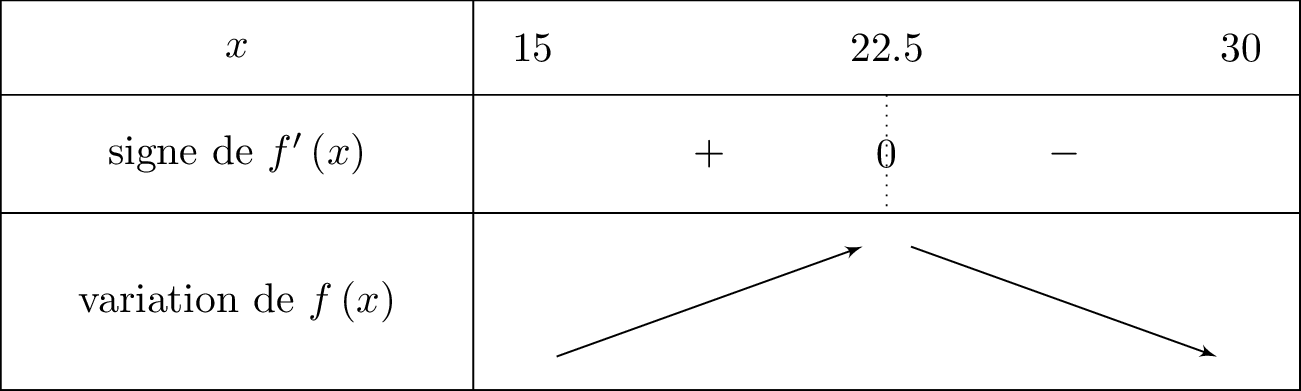
    Étudier les variations de la fonction ff sur l’intervalle [15;30]\left[15; 30\right].

    Correction
    • Si f′f' est négative sur [a;b]\left[a;b\right] alors ff est décroissante sur [a;b]\left[a;b\right].
    • Si f′f' est positive sur [a;b]\left[a;b\right] alors ff est croissante sur [a;b]\left[a;b\right].
    Nous savons que : f′(x)=−4x+90f'\left(x\right)=-4x+90
    Ici la dérivée est une fonction du 11er degré.
    Pour étudier son signe, nous allons résoudre l'inéquation f′(x)≥0f'\left(x\right)\ge 0.
    En effet, en résolvant f′(x)≥0f'\left(x\right)\ge 0, on déterminera ainsi l'intervalle sur lequel la dérivée est positive ou nulle.
    Il vient alors que :
    f′(x)≥0f'\left(x\right)\ge 0 équivaut successivement à
    −4x+90≥0-4x+90\ge 0
    −4x≥−90-4x\ge -90
    x≤−90−4x\le \frac{-90}{-4} . Attention : on change le sens de l’ineˊquation car on divise par un neˊgatif.{\color{red}\text{Attention : on change le sens de l'inéquation car on divise par un négatif.}}
    x≤22,5x\le 22,5
    Cela signifie que l'on va mettre le signe ++ dans la ligne de −4x+90-4x+90 lorsque xx sera inférieur ou égale à 22,522,5.
    Il en résulte donc que :
    • si x∈[15;22,5]x\in\left[15;22,5\right] alors f′(x)≥0f'\left(x\right)\ge0 et donc ff est croissante sur cet intervalle.
    • si x∈[22,5;30]x\in\left[22,5;30\right] alors f′(x)≤0f'\left(x\right)\le0 et donc ff est décroissante sur cet intervalle.
    Nous traduisons toutes ces informations dans le tableau de variation ci-dessous :
    Question 3

    Calculer son maximum.

    Correction
    Nous allons compléter le tableau de variation en indiquant toutes les valeurs :
  • f(15)=−2×152+90×15−400f\left(15\right)=-2\times15^{2}+90\times15-400 ainsi f(15)=500f\left(15\right)=500
  • f(22,5)=−2×22,52+90×22,5−400f\left(22,5\right)=-2\times22,5^{2}+90\times22,5-400 ainsi f(22,5)=612,5f\left(22,5\right)=612,5
  • f(30)=−2×302+90×30−400f\left(30\right)=-2\times30^{2}+90\times30-400 ainsi f(30)=500f\left(30\right)=500
    • Le maximum est atteint en x=22,5x=22,5 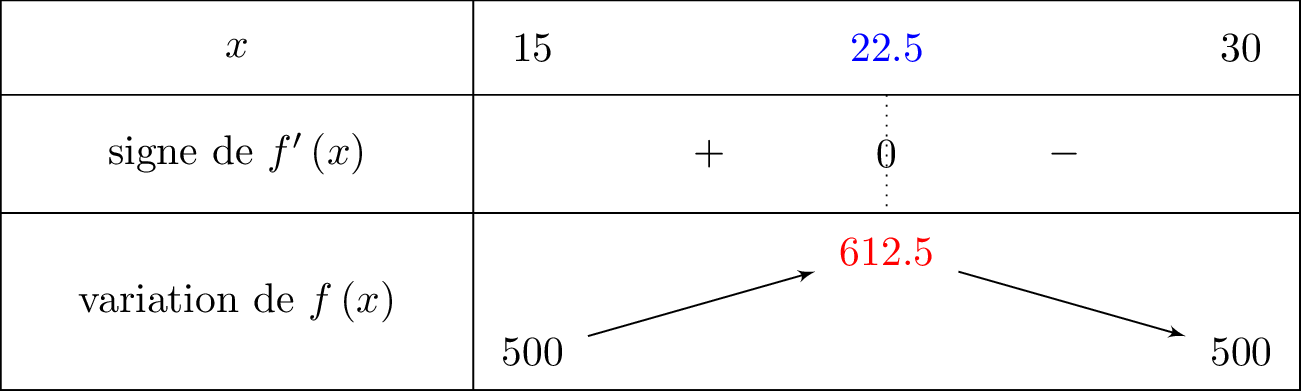et il vaut 612,5612,5
    Question 4
    Les valeurs de xx, arrondies au centième, représentent le nombre de centaines de panneaux solaires produits.

    Pour quelle production le bénéfice est-il maximal? Quelle est alors sa valeur?

    Correction
    Le bénéfice est maximal pour une production de 22502250 panneaux solaires ( car nous avons 22,522,5 centaines ).
    Le bénéfice est alors de 6161 250250 euros. N'oublions pas que le bénéfice de l’entreprise est exprimé en centaine d’euros