Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Comment déterminer l'expression d'une fonction polynôme du troisième degré à partir d'éléments graphiques ou de données - Exercice 2
6 min
20
Question 1
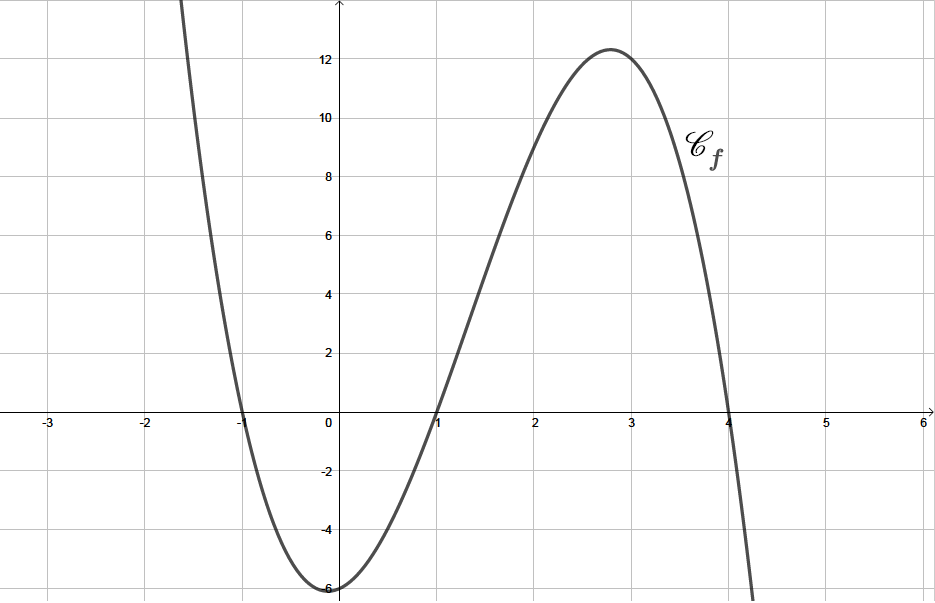
Soit une fonction polynôme de degré dont la représentation graphique est donnée ci-dessous. Déterminer l'expression sous forme factorisée de .
Correction
Soit un réel non nul . Soient , et trois réels.
Soit la fonction polynôme de degré trois définie sur par .
L'équation admet trois solutions que l'on appelle également . Les racines sont alors , et .
D'après la représentation graphique, nous pouvons voir que la courbe passe trois fois par l'axe des abscisses.Soit la fonction polynôme de degré trois définie sur par .
L'équation admet trois solutions que l'on appelle également . Les racines sont alors , et .
Autrement dit, on a : ; et .
Les réels , et sont alors les racines de .
On note alors par exemple que : ; et .
D'après le rappel, nous pouvons alors écrire que :
ou encore :
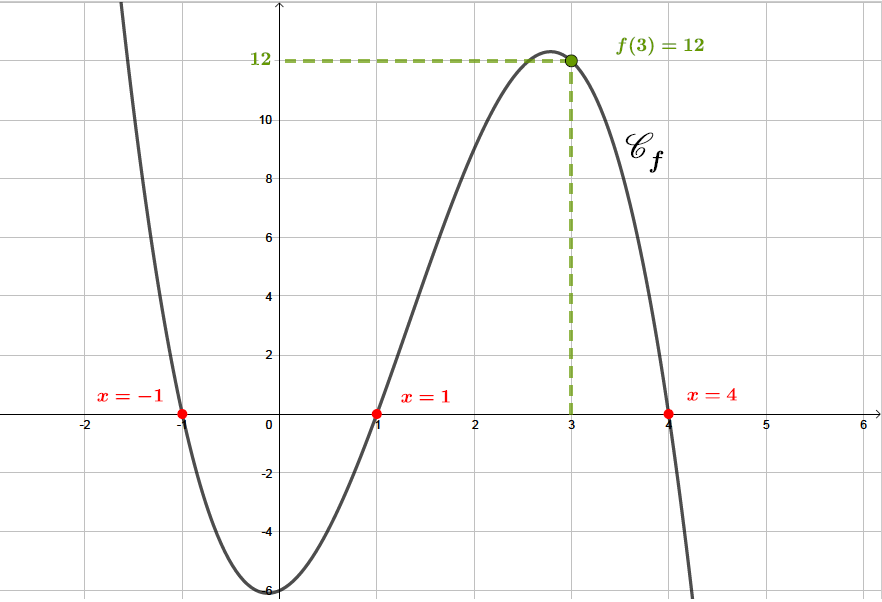
De plus, nous pouvons lire, sur le graphique, que . Cette information va nous permettre de déterminer la valeur du réel .
Il s'ensuit que :
Soit :
La fonction polynôme de degré dont la représentation est donnée ci-dessus s'écrit alors :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.