Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
40 min
65
Un employeur propose à ses salariés, aux choix de chacun, deux modes d'augmentation de leur salaire mensuel.
Question 1
Option A : une augmentation fixe du salaire mensuel, de Euros au er janvier de chaque année.
Lina est embauchée dans l'entreprise avec un salaire de euros. Elle choisit d'être augmentée suivant l'option . On note son salaire après années dans l'entreprise. On a : .
Lina est embauchée dans l'entreprise avec un salaire de euros. Elle choisit d'être augmentée suivant l'option . On note son salaire après années dans l'entreprise. On a : .
Calculer et .
Correction
On a :
ainsi
ainsi
ainsi
ainsi
Question 2
Exprimer en fonction de . En déduire la nature de la suite .
Correction
Soit un entier naturel.
On a : . La suite est alors une suite arithmétique de raison et de premier terme .
On a :
Question 3
Exprimer en fonction de .
Correction
Soit une suite arithmétique. L'expression de en fonction de est :
: lorsque le premier terme vaut . : lorsque le premier terme vaut . : formule avec un premier terme quelconque .
D'après le cours , on sait que :ce qui nous donne donc :
Question 4
Calculer
Correction
Comme alors
Ainsi : .
Ainsi :
Question 5
A partir de combien d'années son salaire sera t-il au moins euros? Une résolution algébrique est bien entendue demandée.
Correction
Nous voulons savoir quand . L'inéquation s'écrit également : .
équivaut succesivement à :
. or , on prend donc l'entier naturel supérieur à cette écriture décimale. Il vient alors que :
Après années dans l'entreprise Lina aura un salaire d'au moins euros.
équivaut succesivement à :
. or , on prend donc l'entier naturel supérieur à cette écriture décimale. Il vient alors que :
Après années dans l'entreprise Lina aura un salaire d'au moins euros.
Question 6
Option B : une augmentation de % du salaire mensuel de l'année précédente au er janvier de chaque année.
Adam est embauché dans l'entreprise avec un salaire de euros. Il choisit d'être augmenté suivant l'option . On note son salaire après années dans l'entreprise. On a : .
Adam est embauché dans l'entreprise avec un salaire de euros. Il choisit d'être augmenté suivant l'option . On note son salaire après années dans l'entreprise. On a : .
Calculer et . Arrondir à l'euros près si besoin.
Correction
On a :
d'où
d'où
d'où
d'où
Question 7
Exprimer en fonction de . En déduire la nature de la suite .
Correction
Chaque année l'augmentation est de % , il nous faut donc multiplier par le coefficient multiplicateur
Ainsi, pour tout entier naturel , on a :
. La suite est alors une suite géométrique de raison et de premier terme .
Ainsi, pour tout entier naturel , on a :
Question 8
Exprimer en fonction de .
Correction
Soit une suite géométrique. L'expression de en fonction de est :
: lorsque le premier terme vaut . : lorsque le premier terme vaut . : formule avec un premier terme quelconque .
D'après le cours , on sait que :ce qui nous donne donc :
Question 9
Calculer . Arrondir à l'euros près.
Correction
Comme alors
Ainsi : .
Ainsi :
Question 10
A partir de combien d'années son salaire sera t-il au moins euros? L'aide de la calculatrice ici est la bienvenue.
Correction
Nous voulons savoir quand . l'inéquation s'écrit également :
Ici nous n'allons pas résoudre algébriquement cette inéquation. Nous allons utiliser la calculatrice. Pour cela, il vous faut entrer l'expression et avec le tableau de valeurs regarder à partir de quelle rang nous avons une valeur supérieur à .
Nous avons les données suivantes :
Ici nous n'allons pas résoudre algébriquement cette inéquation. Nous allons utiliser la calculatrice. Pour cela, il vous faut entrer l'expression et avec le tableau de valeurs regarder à partir de quelle rang nous avons une valeur supérieur à .
Nous avons les données suivantes :
- lorsque nous obtenons
- lorsque nous obtenons
Question 11
A partir de combien d'années dans l'entreprise, le salaire d'Adam sera supérieur à celui de Lina.
Correction
Nous allons reprendre le même raisonnement que la question précédente. Nous allons entrer les expressions et et avec le tableau de valeurs regarder à partir de quelle rang le salaire d'Adam sera supérieur à celui de Lina.
Nous avons les données suivantes :
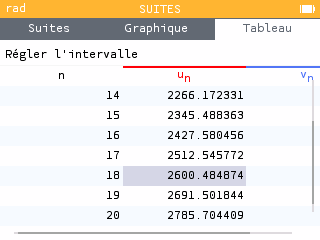
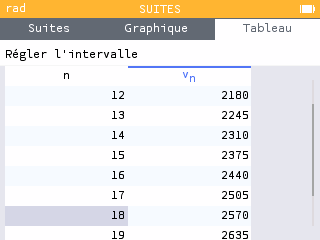
Nous avons les données suivantes :
- lorsque Lina aura un salaire de euros et Adam un salaire de
- lorsque Lina aura un salaire de euros et Adam un salaire de


Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.