Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types - Exercice 3
25 min
45
Une grande coopération agricole fait le bilan de sa production de pommes en . Elle regroupe fermes . Pour chacune d'elles, on note la production de pommes (en Tonnes). On obtient les résultats suivants :
Question 1

Déterminer le premier quartile de la série.
Correction
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
On va commencer par définir les effectifs cumulés croissants (ECC).
Pour déterminer le er quartile, on commence par calculer ce qui donne .
Le er quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à tonnes )
Question 2
Déterminer le troisième quartile de la série.
Correction

Le ème quartile, noté , correspond à la ème valeur de la série ordonnée (on arrondi toujours par excès si son écriture est décimal).
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à tonnes )
Question 3
Déterminer la médiane de la série.
Correction

Ici, est pair, donc on n'écrira pas que la médiane, notée , correspond à la ème valeur de la série ordonnée.
Dans le cas où est pair, on agit de la sorte.
On calcule .
Puis on indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :
Question 4
Tracer le diagramme en boîte correspondant à la série .
Correction
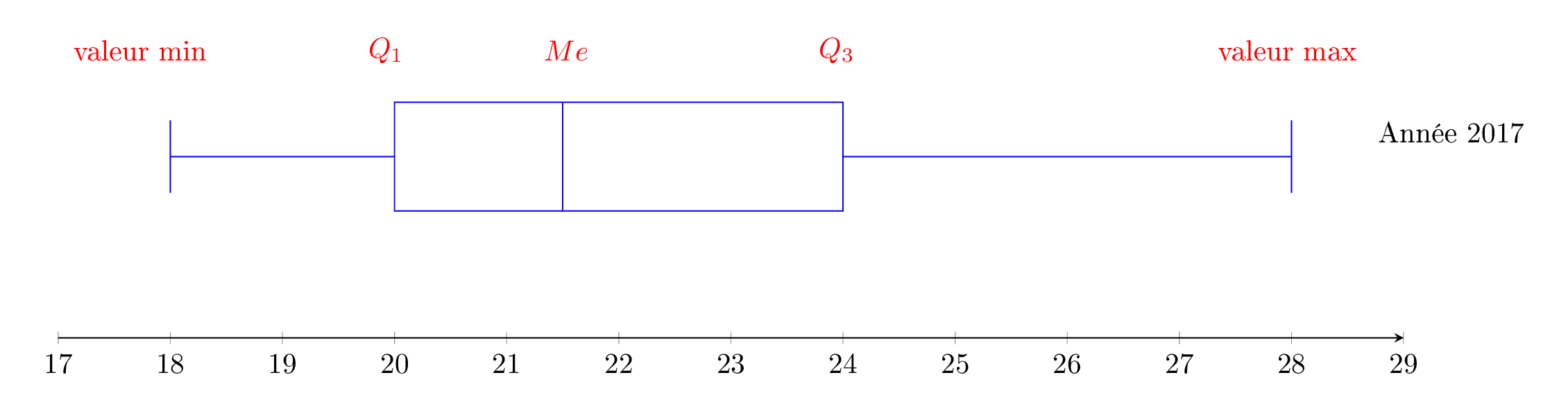
Question 5
Le responsable de la coopération agricole a retrouvé le diagramme en boite de l'année , représenté ci-dessous : 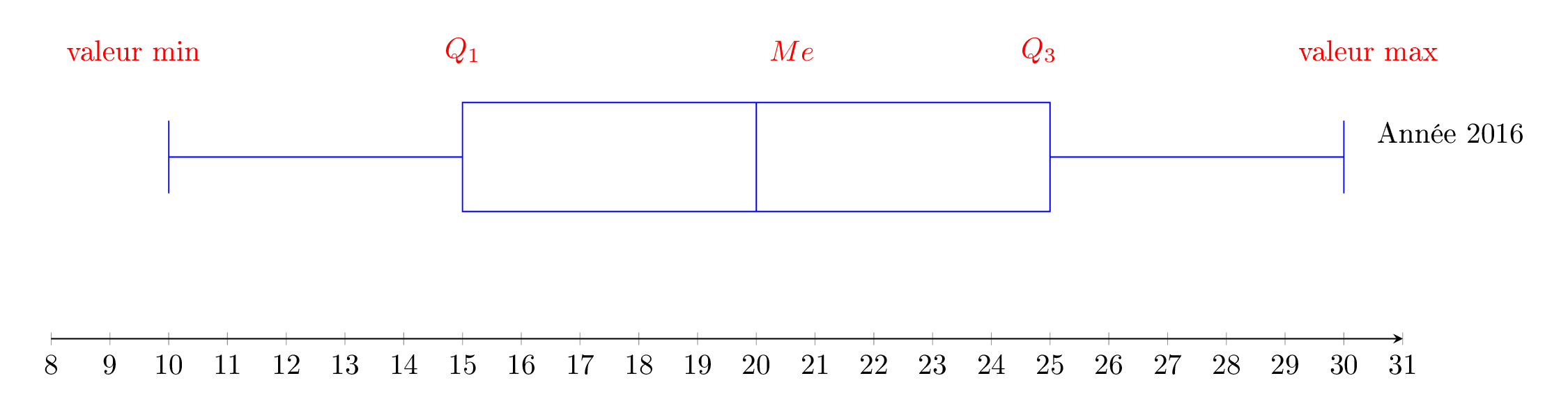

En , à quel pourcentage peut-on estimer la part du nombres de fermes ayant produit tonnes de pommes ou plus? tonnes ou moins de pommes.
Correction
En , au moins des ruches ont produit tonnes de pommes ou plus car le troisième quartile de la série en est .
En , au moins des ruches ont produit tonnes de pommes ou moins car la médiane de la série en est .
En , au moins des ruches ont produit tonnes de pommes ou moins car la médiane de la série en est .
Question 6
A l'aide des deux diagrammes en boîte, comparer la production des deux années.
Correction
En , l'écart interquartile est plus faible qu'en ( en , en ), la production a donc été plus régulière en qu'en .
La médiane de étant égale au premier quartile de (égaux à ), cela signifie qu'en , au mois des fermes ont produit plus de tonnes de pommes, alors qu'en le pourcentage passe à au moins .
Globalement, on peut donc estimer la production meilleure en qu'en .
La médiane de étant égale au premier quartile de (égaux à ), cela signifie qu'en , au mois des fermes ont produit plus de tonnes de pommes, alors qu'en le pourcentage passe à au moins .
Globalement, on peut donc estimer la production meilleure en qu'en .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.