Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 2
20 min
40
Soit le trinôme avec et
Les propositions suivantes sont-elles vraies ou fausses? Justifier bien entendu.
Les propositions suivantes sont-elles vraies ou fausses? Justifier bien entendu.
Question 1
Si et sont de signes opposés, le trinôme a toujours des racines.
Correction
Nous savons que le discriminant est .
Si et sont de signes opposés alors le produit est obligatoirement négatif.
Ainsi, on peut écrire que :
De ce fait :
équivaut successivement à :
( le fait de multiplier par un nombre négatif change le sens de l'inégalité ).
Nous allons maintenant rajouter qui est positif.
Soit .
Il en résulte donc que l'équation admet donc deux racines réelles distinctes.
Question 2
Si pour tout réel , alors .
Correction
Le trinôme étant strictement négatif, cela signifie que la parabole ne passe jamais pas l'axe des abscisses.
Il en résulte que l'équation n'admet aucune racine réelle. Cela est donc équivalent à dire que .
Question 3
Si alors pour tout réel , .
Correction
Prenons l'exemple du trinôme
Calcul du discriminant
Ainsi :
Donc
Comme alors l'équation n'admet pas de racines réelles.
Le tableau de signe du trinôme du second degré va dépendre du signe de .
- Si , la parabole est tourné vers le haut c'est-à-dire que est du signe de et ne passe jamais par l'axe des abscisses.
- Si , la parabole est tourné vers le bas c'est-à-dire que est du signe de et ne passe jamais par l'axe des abscisses.
Il en résulte donc que :
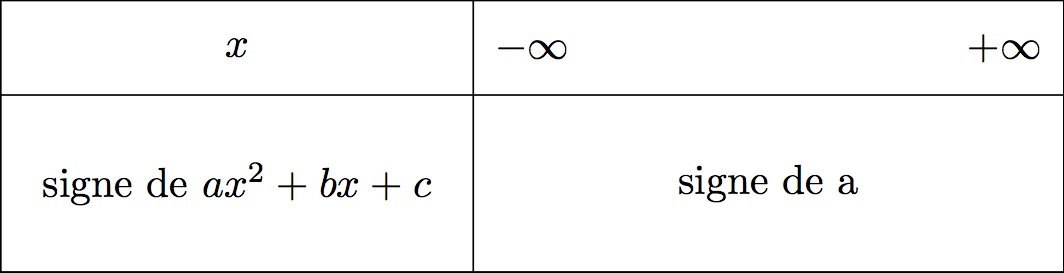
Il vient alors que :
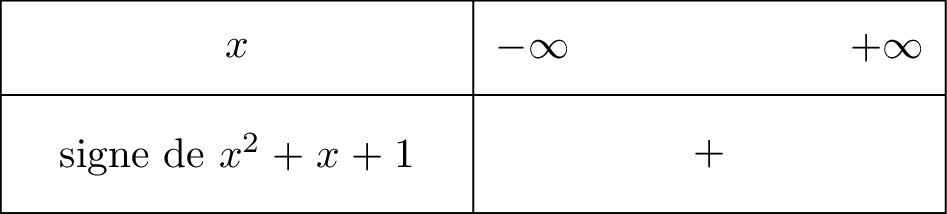
Question 4
Si le trinôme du ème degré a pour racines et , alors il est définit uniquement pour tout par :
Correction
Forme factorisée d'un trinôme du second degré.
Si le trinôme du ème degré a pour racines et , il se factorise sous la forme : où est un réel quelconque et ce n'est pas obligatoirement .- Si et que nous connaissons les racines et , alors la factorisation est de la forme .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.