Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 4
25 min
45
Question 1
Un constructeur de moto électrique décide de faire un coût de publicité en proposant des motos à euros l'unité. Il peut produire au maximum motos. Les coûts de fabrication sont données par la formule : où est exprimé en milliers et est exprimé en millions d'euros.
Quel est le coût fixe supporté par l'entreprise?
Correction
- On appelle coût fixe, le coût que supporte l’entreprise même si la production est nulle.
Ainsi :
Les coûts fixes de l’entreprise s'élèvent à millions d'euros.
Question 2
Déterminer la production de motos à partir de laquelle le cout de production est supérieur à millions.
Correction
Tout d'abord la fonction est définie sur l'intervalle .
Il nous faut résoudre l'inéquation .
équivaut successivement à :
1ère étape : On définit les valeurs , et .
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors la fonction admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme et que nous connaissons les racines et , le tableau du trinôme du second degré dépend du signe de .
Dans notre situation, , la parabole est tournée vers le haut c'est-à-dire que la fonction est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Il vient alors que :
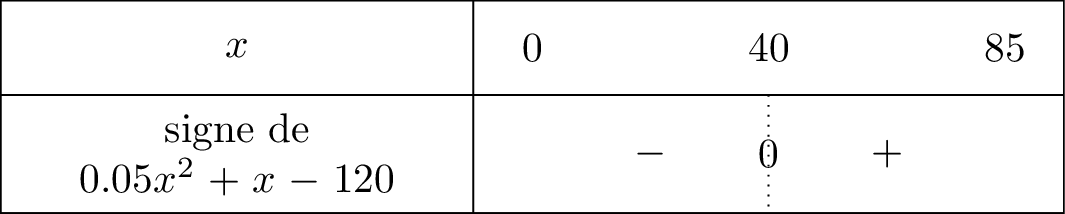 Finalement, les coûts de production sont supérieurs à millions à partir de motos fabriquées et jusqu'à motos fabriquées.
Finalement, les coûts de production sont supérieurs à millions à partir de motos fabriquées et jusqu'à motos fabriquées.
Il nous faut résoudre l'inéquation .
équivaut successivement à :
1ère étape : On définit les valeurs , et .
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors la fonction admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme et que nous connaissons les racines et , le tableau du trinôme du second degré dépend du signe de .
Dans notre situation, , la parabole est tournée vers le haut c'est-à-dire que la fonction est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Il vient alors que :
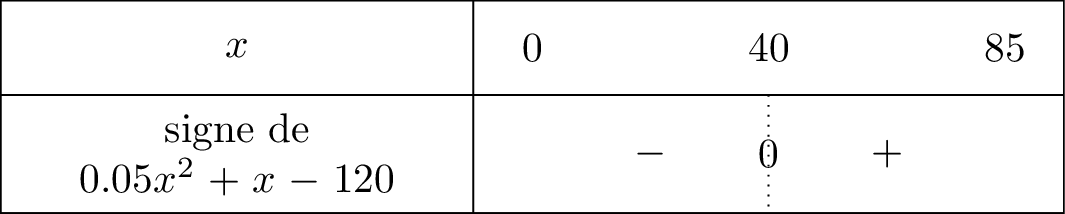
Question 3
A combien s'élève la recette pour une telle production?
Correction
Une montant est vendue euros. Il faut produire motos pour avoir un coût de production égale à millions.
Ainsi : .
La recette pour motos fabriquées est de millions d'euros.
Ainsi : .
La recette pour motos fabriquées est de millions d'euros.
Question 4
Exprimer, en fonction de , la recette notée , en millions d'euros.
Correction
Chaque moto est vendue milliers d'euros. Il en résulte donc que :
Question 5
Exprimer, en fonction de , le bénéfice notée , en millions d'euros.
Correction
- Bénéfice Recette Coût de production
équivaut successivement à :
Question 6
Dans quel intervalle doit se situer la quantité de motos produites pour réaliser un bénéfice?
Correction
Il nous faut résoudre l'inéquation .
équivaut successivement à :
1ère étape : On définit les valeurs , et .
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors la fonction admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme et que nous connaissons les racines et , le tableau du trinôme du second degré dépend du signe de .
Dans notre situation, , la parabole est tournée vers le bas c'est-à-dire que la fonction est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Il vient alors que :
 En produisant entre et motos, le bénéfice sera positif.
En produisant entre et motos, le bénéfice sera positif.
équivaut successivement à :
1ère étape : On définit les valeurs , et .
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors la fonction admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme et que nous connaissons les racines et , le tableau du trinôme du second degré dépend du signe de .
Dans notre situation, , la parabole est tournée vers le bas c'est-à-dire que la fonction est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Il vient alors que :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.