Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 2
15 min
30
Le plan est muni d'un repère orthonormal.
On considère la fonction définie sur par et on note sa représentation graphique.
On considère la fonction définie sur par et on note sa représentation graphique.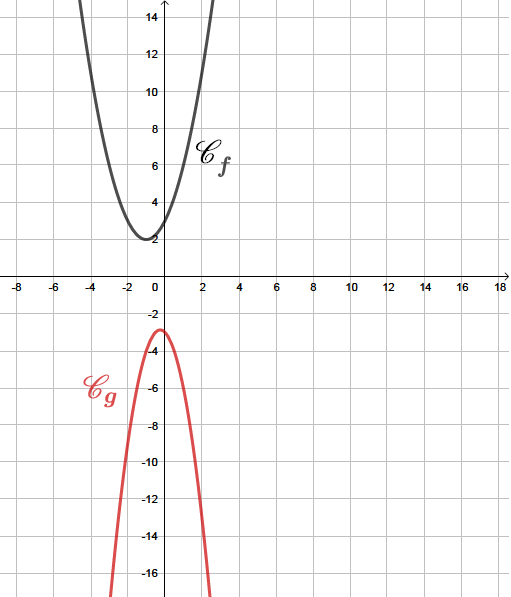
On considère la fonction définie sur par et on note sa représentation graphique.
On considère la fonction définie sur par et on note sa représentation graphique.

Question 1
On pose : .
Exprimer en fonction de .
Correction
équivaut successivement à :
Ainsi :
Ainsi :
Question 2
Etudier le signe de et en déduire la position relative entre et .
Correction
Nous allons étudier dans le signe de la fonction : .
1ère étape : On définit les valeurs , et .
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors l'équation n'admet pas de racines réelles.
Autrement dit, il n'y a pas de solution à l'équation car .
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme , le tableau de signe du trinôme du second degré va dépendre du signe de .
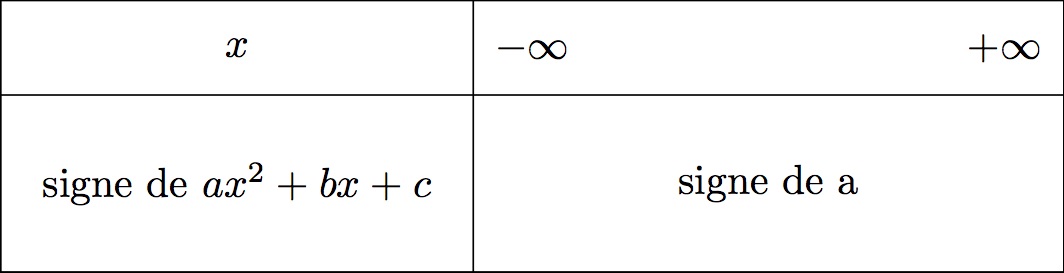 Dans notre situation, , la parabole est tournée vers le haut c'est-à-dire que est du signe de et ne passe jamais par l'axe des abscisses.
Dans notre situation, , la parabole est tournée vers le haut c'est-à-dire que est du signe de et ne passe jamais par l'axe des abscisses.
Il vient alors que :
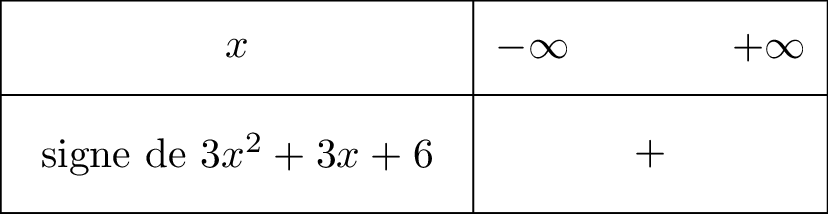 Sur l'intervalle nous avons autrement dit ou encore .
Sur l'intervalle nous avons autrement dit ou encore .
Cela signifie que la courbe est au-dessus de la droite .

1ère étape : On définit les valeurs , et .
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Ainsi :
Donc
3ème étape : Calcul des racines suivant le signe du discriminant .
Comme alors l'équation n'admet pas de racines réelles.
Autrement dit, il n'y a pas de solution à l'équation car .
4ème étape : Le tableau de signe du trinôme du second degré qui dépend du signe du discriminant .
Comme , le tableau de signe du trinôme du second degré va dépendre du signe de .
- Si , la parabole est tourné vers le haut c'est-à-dire que est du signe de et ne passe jamais par l'axe des abscisses.
- Si , la parabole est tourné vers le bas c'est-à-dire que est du signe de et ne passe jamais par l'axe des abscisses.

Il vient alors que :
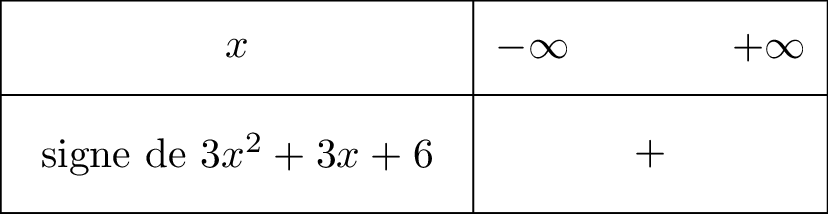
Cela signifie que la courbe est au-dessus de la droite .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.