Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 5
20 min
40
Question 1
Résoudre, dans , l'inéquation .
Correction
Commençons à étudier le signe du numérateur puis celui du dénominateur.
On regroupera ensuite l'ensemble des informations obtenues dans un tableau de signe.
Première étape : étude du signe du numérateur .
Calcul du discriminant ainsi :
Comme alors le numérateur admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
, la parabole est tournée vers le bas c'est-à-dire que le numérateur est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Ainsi :
 Deuxième étape : étude du signe du dénominateur .
Deuxième étape : étude du signe du dénominateur .
En ce qui concerne maintenant le signe du dénominateur, on a :
Cela signifie que l'on va mettre le signe + dans la ligne de lorsque sera supérieur ou égale à .
On traduit cela maintenant dans le tableau de signe complet, cela nous donne :
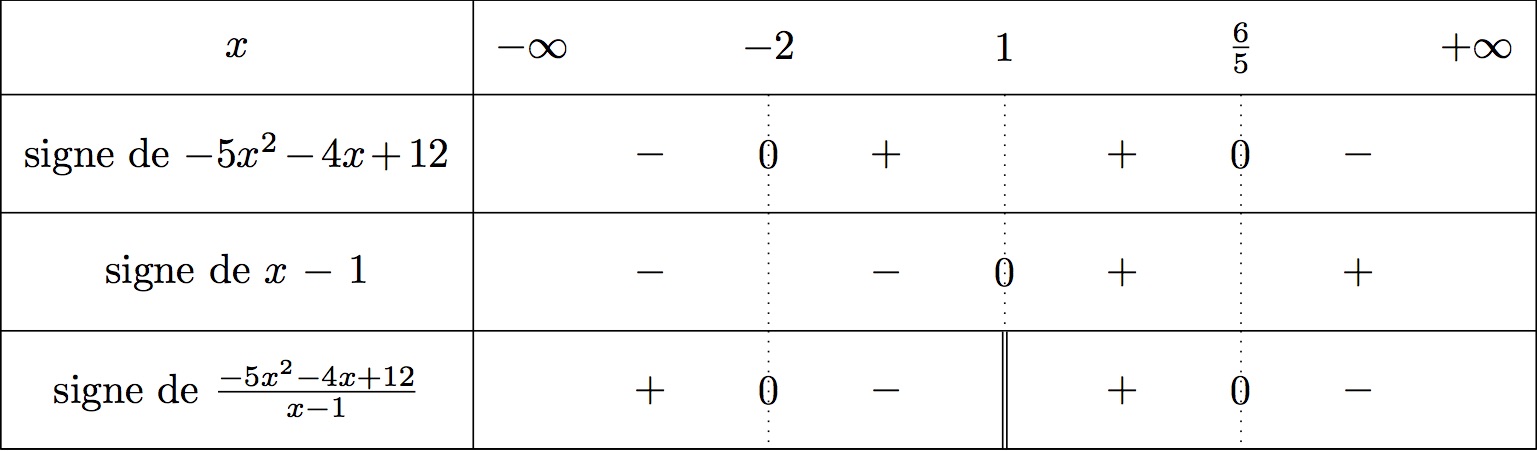
Il en résulte que les solutions de l'inéquation sont alors :
On regroupera ensuite l'ensemble des informations obtenues dans un tableau de signe.
Première étape : étude du signe du numérateur .
Calcul du discriminant ainsi :
Comme alors le numérateur admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
, la parabole est tournée vers le bas c'est-à-dire que le numérateur est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Ainsi :

En ce qui concerne maintenant le signe du dénominateur, on a :
Cela signifie que l'on va mettre le signe + dans la ligne de lorsque sera supérieur ou égale à .
On traduit cela maintenant dans le tableau de signe complet, cela nous donne :

Il en résulte que les solutions de l'inéquation sont alors :
Question 2
On considère la fonction définie sur par et la fonction , définie sur par .
On note et leurs représentations graphiques dans un repère.
On note et leurs représentations graphiques dans un repère.
Déterminer les valeurs de pour lesquelles est au-dessus de .
Correction
On cherche ici la position relative entre les courbes et .
Pour cela, il nous faut donc étudier le signe de la fonction .
Il vient alors que :
équivaut successivement à :
Nous allons tout mettre au même dénominateur.
Or la fonction est celle que l'on a étudiée à la question .
Ainsi d'après la question , on a :
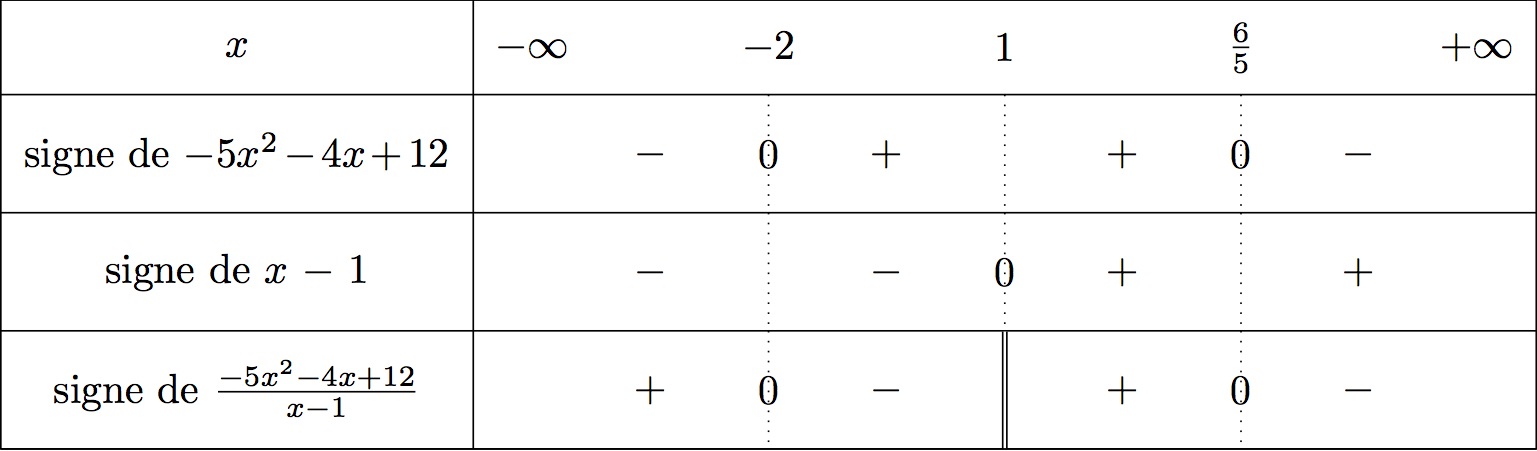 Les valeurs de pour lesquelles est au-dessus de sont déterminées à l'aide de l'inéquation , autrement dit quand .
Les valeurs de pour lesquelles est au-dessus de sont déterminées à l'aide de l'inéquation , autrement dit quand .
Ainsi :
Autrement dit sur les intervalles et , la courbe est au-dessus de .
Pour cela, il nous faut donc étudier le signe de la fonction .
Il vient alors que :
équivaut successivement à :
Nous allons tout mettre au même dénominateur.
Or la fonction est celle que l'on a étudiée à la question .
Ainsi d'après la question , on a :

Ainsi :
Autrement dit sur les intervalles et , la courbe est au-dessus de .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.