Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 4
25 min
40
est un rectangle de cotés et .
Sur chacun des côtés, on place les points , , et respectivement sur , , et tel que en cm.
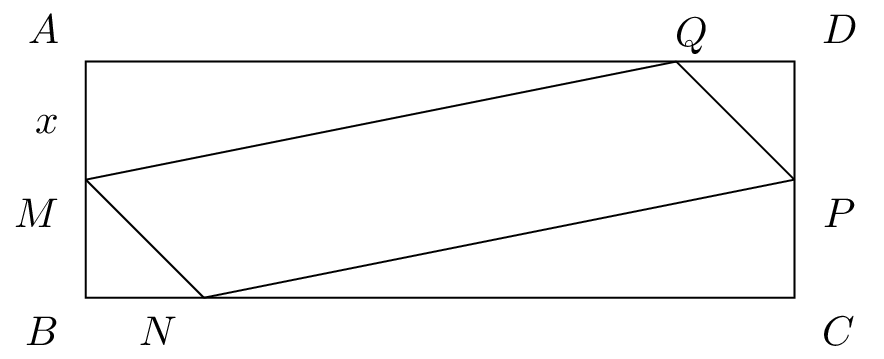
Sur chacun des côtés, on place les points , , et respectivement sur , , et tel que en cm.

Question 1
Sur quel intervalle varie ?
Justifier.
Justifier.
Correction
On sait que :
et
Le segment est inférieure ou égale à la mesure du segment .
Ainsi :
et
Le segment est inférieure ou égale à la mesure du segment .
Ainsi :
Question 2
On note l'aire du quadrilatère .
Exprimez en fonction de .
Correction
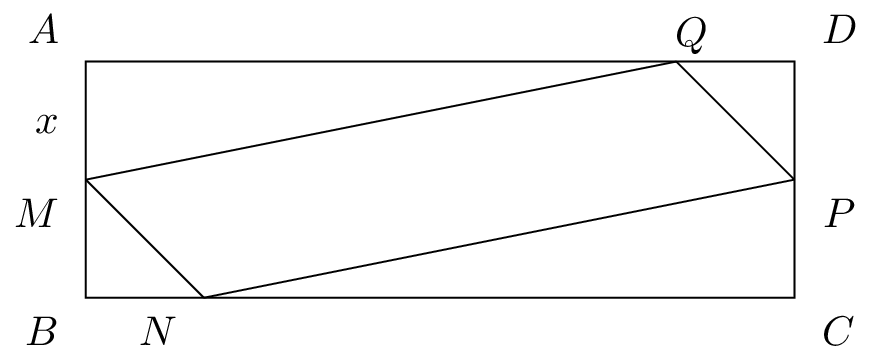
L'aire du triangle rectangle en :
L'aire du triangle rectangle en :
L'aire du triangle rectangle en :
L'aire du triangle rectangle en :
Maintenant, calculons l'aire du quadrilatère :
Question 3
On veut déterminer les valeurs de , si elles existent, pour lesquelles l'aire du quadrilatère est égale à .
Montrer que cela revient à résoudre l'équation .
Correction
On sait que et nous voulons que .
Il en résulte que :
On divise tout par deux, et on obtient :
Il en résulte que :
On divise tout par deux, et on obtient :
Question 4
Résoudre l'équation .
Correction
Résolvons :
Calcul du discriminant
Ainsi :
Comme alors l'équation admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
Les racines de l'équation sont donc :
Calcul du discriminant
Ainsi :
Comme alors l'équation admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
Les racines de l'équation sont donc :
Question 5
Répondre à la question posée.
Correction
L'aire du quadrilatère est égale à lorsque ou alors lorsque .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.