Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Forme canonique et variation - Exercice 3
10 min
15
Soit la fonction définie sur par .
Question 1
Déterminer la forme canonique de la fonction polynôme du second degré .
Correction
Nous allons vous proposer pour répondre à cette question. A vous de choisir celle qui vous correspond le mieux .
Il vient alors que : d'où :
Calcul de
Il vient alors que :
Ainsi, pour tout réel , la est .
équivaut successivement à :
On va développer , ce qui nous donne : .
Toute fonction polynôme de degré définie sur par avec , peut s'écrire sous la forme :
On définit les valeurs , et .- avec et
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Il vient alors que : d'où :
Calcul de
Il vient alors que :
Ainsi, pour tout réel , la est
équivaut successivement à :
On va développer , ce qui nous donne :
Question 2
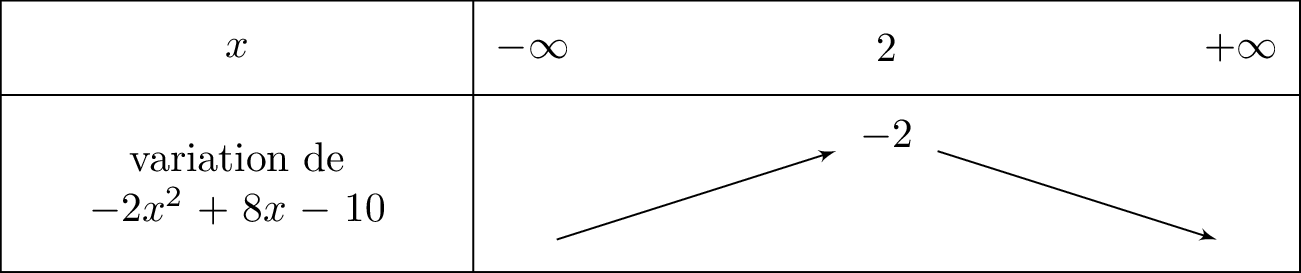
En déduire le tableau de variation de .
Justifier.
Justifier.
Correction
La d'une fonction polynôme du second degré est :
où correspond au sommet de la parabole.
Si alors le tableau de variation de est :
 Si alors le tableau de variation de est :
Si alors le tableau de variation de est :

A l'aide de la forme canonique, on détermine facilement le sommet de la parabole.où correspond au sommet de la parabole.
Si alors le tableau de variation de est :


Or : .
On note le sommet de la parabole.
Ici, nous avons , et .
, la parabole est tournée vers le bas et est le sommet de la parabole (plus précisément un maximum).
Le tableau de variation est alors :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.