Exercices types : mise en situation sous forme de problèmes $$\red{\text{(sans discriminant)}}$$ - Exercice 3

Soit $$f\left(x\right)=-2x^{2} +4x+1$$
Pour déterminer la hauteur maximale, il faut donner la forme canonique de $$f$$ puis ensuite dresser le tableau de variation de $$f$$.
1^ère étape : On définit les valeurs $$a$$, $$b$$ et $$c$$.

• $$a=$$ nombre devant $$x^{2}$$ d'où $$a=-2$$
• $$b=$$ nombre devant $$x$$ d'où $$b=4$$
• $$c=$$ nombre seul d'où $$c=1$$

2^ème étape : Calcul de $$\alpha =\frac{-b}{2a}$$
Il vient alors que : $$\alpha =\frac{-4}{2\times\left(-2\right)}$$ d'où :
3^ème étape : Calcul de $$\beta =f\left(\alpha \right)$$
Il vient alors que :
$$\beta =f\left(1 \right)$$
$$\beta =-2\times 1^{2} +4\times 1+1$$
$$\beta =-2\times 1+4+1$$
$$\beta =-2+4+1$$

4^ème étape : Le tableau de variation de $$f$$.
La forme canonique de $$f$$ est alors : $$f\left(x\right)=-2\left(x-1 \right)^{2} +3$$
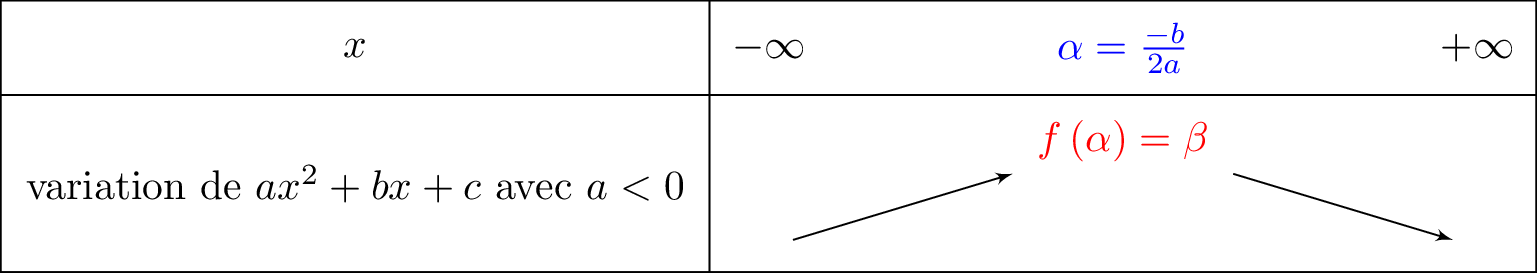
Ici : $$a=-2<0$$. La parabole est tournée vers le bas. Le tableau de variation est alors donné ci-dessous :
La puce réalise un saut maximal de $$3$$ cm de hauteur .