Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : mise en situation sous forme de problèmes - Exercice 2
6 min
15
Une entreprise vend des logiciels (licences spécialisées) mathématiques pour les lycées. Le bénéfice réalisé par cette vente de logiciels, en une semaine, est modélisée par la fonction . Le bénéfice est exprimé en euros.
L'entreprise ne peut pas fournir plus de logiciels par semaine, on aura ainsi :
L'entreprise ne peut pas fournir plus de logiciels par semaine, on aura ainsi :
Question 1
Calculer le bénéfice pour licences.
Correction
Il nous faut calculer .
L'entreprise réalisera un bénéfice de euros pour une vente de licences.
L'entreprise réalisera un bénéfice de euros pour une vente de licences.
Question 2
Combien de licences l’entreprise doit fabriquer et vendre par semaine pour avoir un bénéfice maximal ?
Correction
Pour déterminer le bénéfice maximal, nous allons commencer par donner la forme canonique de :
Toute fonction polynôme de degré définie sur par avec , peut s'écrire sous la forme :1ère étape : On définit les valeurs , et .
Il vient alors que : d'où :
3ème étape : Calcul de
Il vient alors que :
Ainsi, pour tout réel , la forme canonique est : ce qui nous donne : .
Maintenant, que nous avons la forme canonique de la fonction , nous allons pouvoir dresser le tableau de variation de .
Comme , la parabole est tournée vers le bas. Il en résulte donc que :  Finalement, pour une production de licences, le bénéfice maximal est alors de euros.
Finalement, pour une production de licences, le bénéfice maximal est alors de euros.
Toute fonction polynôme de degré définie sur par avec , peut s'écrire sous la forme :
- avec et
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Il vient alors que : d'où :
3ème étape : Calcul de
Il vient alors que :
Ainsi, pour tout réel , la forme canonique est : ce qui nous donne :
Maintenant, que nous avons la forme canonique de la fonction , nous allons pouvoir dresser le tableau de variation de .
- Soit la forme canonique avec et . Si , la parabole est tournée vers le bas et le tableau de variation est comme suit :
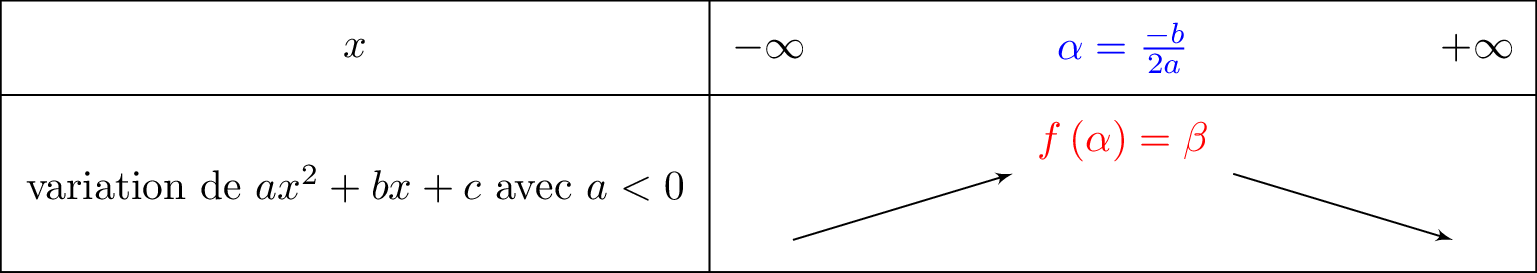

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.