Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : lien entre la forme canonique ; la forme factorisée et la représentation graphique - Exercice 1
5 min
15
On donne ci-dessous la courbe représentative d'une fonction polynôme du second degré.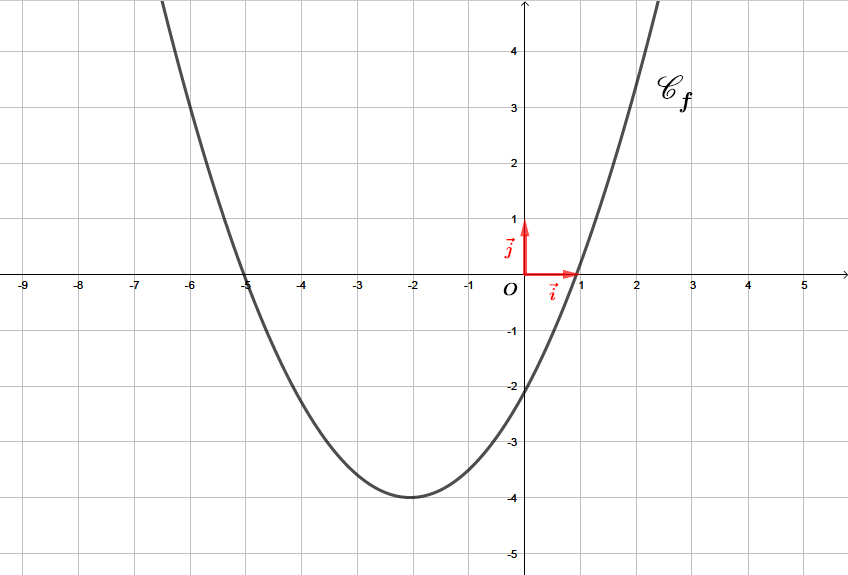

Question 1
Déterminer l'expression de la forme canonique de .
Correction
La d'une fonction polynôme du second degré est :
où correspond au sommet de la parabole.
où correspond au sommet de la parabole.
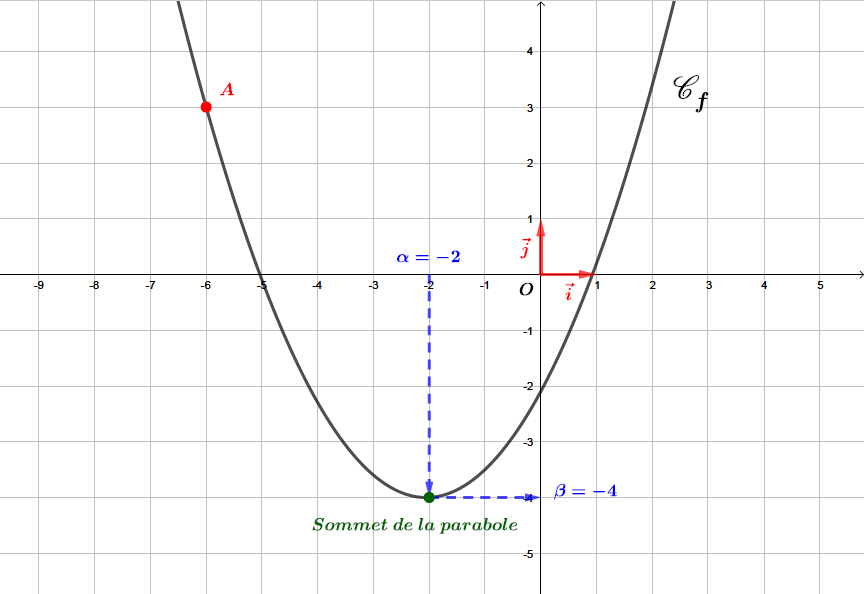
Il vient alors que : et
D'après notre rappel, la forme canonique de s'écrit :
Ce qui nous donne alors :
Il reste maintenant à déterminer la valeur de . Pour cela, le point appartient à la parabole . Nous pouvons traduire cette donnée par
Il nous suffit alors de remplacer tous les par dans l'expression de afin d'obtenir la valeur de .
Ainsi :
équivaut successivement à :
Soit :
Finalement , l'expression de la forme canonique de est :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.