Exercices types : Comment bien choisir la forme adaptée d'une fonction polynôme du second degré $$\red{\text{(sans discriminant)}}$$ - Exercice 2

$$f\left(x\right)=2\left(x-3\right)\left(x+2\right)$$
$$f\left(x\right)=2\left(x\times x+x\times 2+\left(-3\right)\times x+\left(-3\right)\times 2\right)$$
$$f\left(x\right)=2\left(x^{2} +2x-3x-6\right)$$
$$f\left(x\right)=2\left(x^{2} -x-6\right)$$
Ainsi : Nous savons que $$f\left(x\right)=2x^{2} -2x-12$$ . Nous avons $$a=2\ne 0$$ ; $$b=-2$$ et $$c=-12$$ .
Il en résulte donc que $$f$$ est une fonction polynôme du second degré.
La forme $$f\left(x\right)=2x^{2} -2x-12$$ est$$\red{\text{ appelée la forme développée de}}$$ $$\red{f}$$ .

Soit $$f\left(x\right)=2x^{2} -2x-12$$
1^ère étape : On définit les valeurs $$a$$, $$b$$ et $$c$$.

• $$a=$$ nombre devant $$x^{2}$$ d'où $$a=2$$
• $$b=$$ nombre devant $$x$$ d'où $$b=-2$$
• $$c=$$ nombre seul d'où $$c=-12$$

2^ème étape : Calcul de $$\alpha =\frac{-b}{2a}$$
Il vient alors que : $$\alpha =\frac{-\left(-2\right)}{2\times2}$$ d'où :
3^ème étape : Calcul de $$\beta =f\left(\alpha \right)$$
Il vient alors que :
$$\beta =f\left(\frac{1}{2} \right)$$
$$\beta =2\times\left(\frac{1}{2} \right)^{2} -2\times\left(\frac{1}{2} \right)-12$$

Ainsi, pour tout réel $$x$$, la forme canonique est : $$f\left(x\right)=a\left(x-\alpha \right)^{2} +\beta$$ ce qui nous donne :

Il nous faut donc calculer $$f\left(0\right)$$
Nous allons utiliser la forme $$f\left(x\right)=2x^{2} -2x-12$$. Ainsi :
$$f\left(0\right)=2\times0^{2} -2\times0-12$$
D'où :

Il nous faut résoudre, dans $$\mathbb{R}$$, l'équation $$f\left(x\right)=0$$
Il faudra utiliser la forme factorisée de $$f$$, c'est à dire : $$f\left(x\right)=2\left(x-3\right)\left(x+2\right)$$ . D'où :
$$f\left(x\right)=0$$ équivaut successivement à :
$$2\left(x-3\right)\left(x+2\right)=0$$ . $$\purple{\text{Il s'agit d'une équation produit nul}}$$ $$\;\;$$ Comme $$2>0$$, on a :
$$x-3=0$$ ou $$x+2=0$$

$$\red{\text{D'une part :}}$$ résolvons $$x-3=0$$ qui donne $$x=3$$

$$\red{\text{D'autre part :}}$$ résolvons $$x+2=0$$ qui donne $$x=-2$$

Les solutions de l'équation $$f\left(x\right)=0$$ sont alors :

Pour résoudre l'équation $$f\left(x\right)=-\frac{25}{2}$$, il faudra utiliser la forme canonique de $$f$$, c'est à dire : $$f\left(x\right)=2\left(x-\frac{1}{2} \right)^{2}-\frac{25}{2}$$ . D'où :
$$f\left(x\right)=-\frac{25}{2}$$
$$2\left(x-\frac{1}{2} \right)^{2}-\frac{25}{2}=-\frac{25}{2}$$
$$2\left(x-\frac{1}{2} \right)^{2}=0$$
$$\left(x-\frac{1}{2} \right)^{2}=\frac{0}{2}$$
$$\left(x-\frac{1}{2} \right)^{2}=0$$
$$x-\frac{1}{2}=0$$
$$x=\frac{1}{2}$$
La solution de l'équation $$f\left(x\right)=-\frac{25}{2}$$ est alors :

Il nous faut résoudre l'inéquation : $$f\left(x\right)<0$$
Il faudra utiliser la forme factorisée de $$f$$, c'est à dire : $$f\left(x\right)=2\left(x-3\right)\left(x+2\right)$$ . Nous avons donc besoin du tableau de signe de la fonction $$f$$ .

$$\red{\text{D'une part :}}$$

$$x-3=0\Leftrightarrow x=3$$
Soit $$x\mapsto x-3$$ est une fonction affine croissante car son coefficient directeur $$a=1>0$$. (Cela signifie que la fonction MONTE donc on commencera dans la ligne $$x-3$$ par le signe $$\left(-\right)$$ et dès que l'on dépasse la valeur $$x=3$$ on mettra le signe $$\left(+\right)$$ dans le tableau de signe.)

$$\red{\text{D'autre part :}}$$

$$x+2=0\Leftrightarrow x=-2$$
Soit $$x\mapsto x+2$$ est une fonction affine croissante car son coefficient directeur $$a=1>0$$. (Cela signifie que la fonction MONTE donc on commencera dans la ligne $$x+2$$ par le signe $$\left(-\right)$$ et dès que l'on dépasse la valeur $$x=-2$$ on mettra le signe $$\left(+\right)$$ dans le tableau de signe.)
$$\red{\text{Enfin :}}$$ $$2$$ est strictement positif. On mettra que le signe $$\left(+\right)$$ dans la ligne de $$2$$.
Le tableau du signe du produit est donné ci-dessous :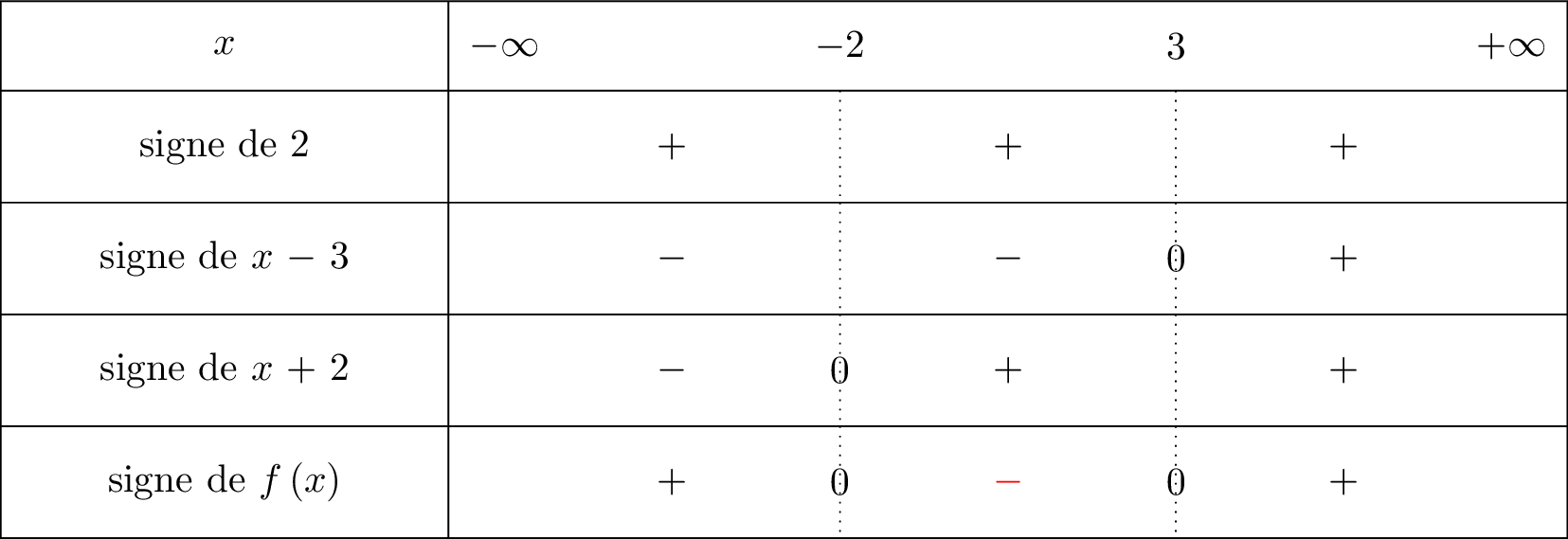Les solution de l'inéquation : $$f\left(x\right)<0$$ sont alors :