Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
20 min
40
Soit la fonction définie sur par .
Question 1
Vérifier que est une fonction polynôme du second degré.
Correction
Nous allons commencer par donner la forme développée de .
Il vient alors que :
équivaut successivement à :
est une fonction polynôme du second degré car ; et
Il vient alors que :
équivaut successivement à :
Une fonction polynôme du second degré est une fonction définie sur de la forme où et sont trois réels avec .
Soit est une fonction polynôme du second degré car ; et
Question 2
Déterminer la forme canonique de .
Correction
Nous allons utiliser la forme développée de .
Soit
Il vient alors que : d'où :
Calcul de
Il vient alors que :
Ainsi, pour tout réel , la est : ce qui nous donne : .
Soit
Toute fonction polynôme de degré définie sur par avec , peut s'écrire sous la forme :
On définit les valeurs , et .- avec et
- nombre devant d'où
- nombre devant d'où
- nombre seul d'où
Il vient alors que : d'où :
Calcul de
Il vient alors que :
Ainsi, pour tout réel , la est : ce qui nous donne :
Question 3
En utilisant la forme la plus adapté de , déterminer :
Le ou les antécédents par la fonction de .
Correction
Pour déterminer le ou les antécédents par la fonction de , il nous faut résoudre l'équation . Il faudra utiliser la forme factorisée de , c'est à dire : . D'où :
équivaut successivement à :
.
Les antécédents de par la fonction sont et .
équivaut successivement à :
.
Les antécédents de par la fonction sont et .
Question 4
L'image de par .
Correction
Il nous faut calculer . Pour cela, nous allons utiliser la forme développée . Ainsi :
L'image de par est égale à .
L'image de par est égale à .
Question 5
L'ensemble des solutions de l'inéquation
Correction
Nous allons utiliser la forme factorisée de afin de résoudre l'inéquation .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
Le tableau du signe de la fonction est donné ci-dessous :
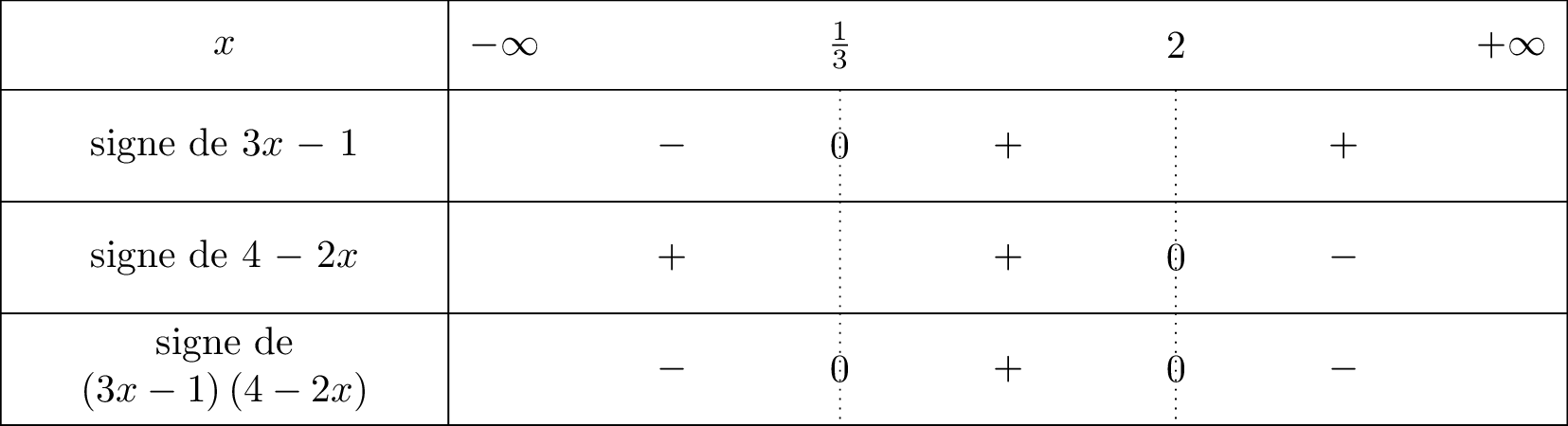 (On utilise la règle des signes pour remplir la dernière ligne.)
(On utilise la règle des signes pour remplir la dernière ligne.)
L'ensemble des solutions de l'inéquation est alors :
Pour étudier le signe d'un produit :
- On étudie le signe de chaque facteur.
- On regroupe dans un tableau le signe de chaque facteur. La première ligne du tableau contenant les valeurs, rangées dans l'ordre croissant, qui annulent chacun des facteurs.
- On utilise la règle des signes pour remplir la dernière ligne
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
Le tableau du signe de la fonction est donné ci-dessous :

L'ensemble des solutions de l'inéquation est alors :
Question 6
Le tableau de variation de .
Correction
Nous allons utiliser la forme canonique de afin de déterminer tableau de variation de .
Nous pouvons dresser le tableau de variation de L'extremum ici est un maximum dont les coordonnées sont
L'extremum ici est un maximum dont les coordonnées sont
La d'une fonction polynôme du second degré est :
où correspond au sommet de la parabole.
Si alors le tableau de variation de est :
 Si alors le tableau de variation de est :
Si alors le tableau de variation de est :
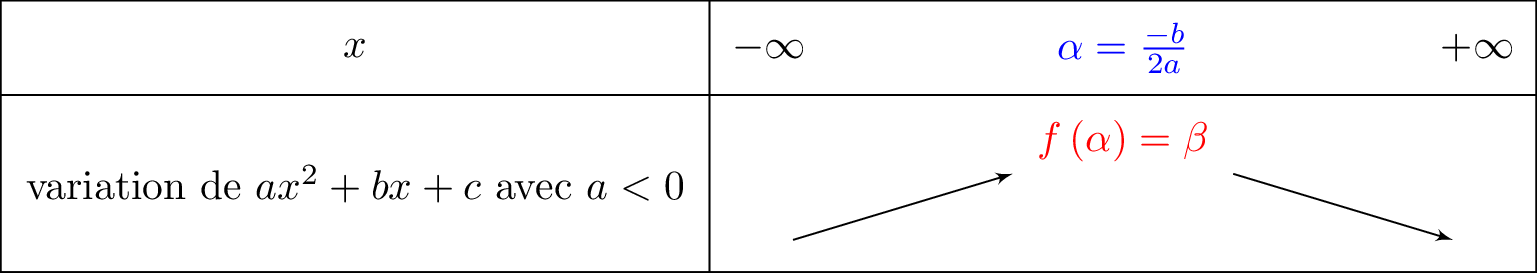
Nous avons nous avons donc ; et où correspond au sommet de la parabole.
Si alors le tableau de variation de est :

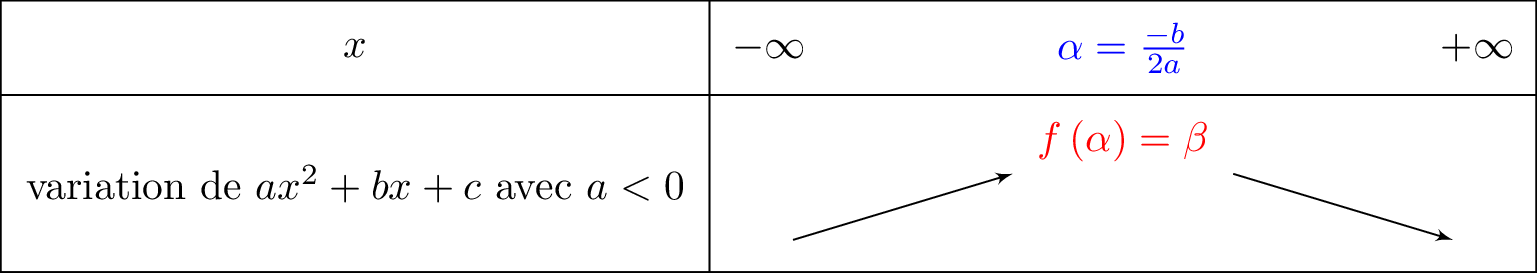
Nous pouvons dresser le tableau de variation de

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.