Probabilités
Intervalle de fluctuation selon la loi binomiale : Application directe de la formule - Exercice 1
1 min
0
Question 1
Soit une variable aléatoire qui suit une loi binomiale de paramètres et . Déterminer l'intervalle de fluctuation au seuil de . Le corrigé fera apparaître les écrans de la calculatrice TEXAS TI 83 Premium CE.
Correction
L'intervalle de fluctuation à d'une fréquence correspondant à la réalisation, sur un échantillon de taille , d'une variable aléatoire X de loi binomiale , est l'intervalle défini par :
1ère cas de figure : A l'aide d'une Texas, nous suivons la procédure comme suit :- est le plus petit entier tel que :
- est le plus petit entier tel que
Touche ou → VAR → Choisir BinomFREP . Il faut ensuite remplir : nbreESSAI : puis et puis écrire Valeur de
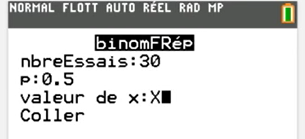
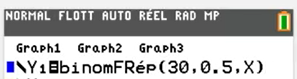
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :


2ème cas de figure : A l'aide d'une Casio graph , nous suivons la procédure comme suit :
Menu TABLE → OPTN → → STAT → DIST → BINM → Bcd
Ensuite il vous faut remplir comme suit à l'écran : BinominalCD(,,) ici on va mettre BinominalCD(,,) puis . Ensuite renseigné pour START : et END : et Step : puis EXE puis
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
- ce qui nous donne
- ce qui nous donne
Question 2
Soit une variable aléatoire qui suit une loi binomiale de paramètres et . Déterminer l'intervalle de fluctuation au seuil de . Le corrigé fera apparaître les écrans de la calculatrice Graph +.
Correction
L'intervalle de fluctuation à d'une fréquence correspondant à la réalisation, sur un échantillon de taille , d'une variable aléatoire X de loi binomiale , est l'intervalle défini par :
1ère cas de figure : A l'aide d'une Texas, nous suivons la procédure comme suit :- est le plus petit entier tel que :
- est le plus petit entier tel que
Touche ou → VAR → Choisir BinomFREP puis écrire BinomFREP(,,)
Puis faire 2nde → Fenêtre puis remplir DébutTbl : et Tbl : et enfin 2nde → Graphe
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
- ce qui nous donne
- ce qui nous donne
2ème cas de figure : A l'aide d'une Casio graph , nous suivons la procédure comme suit :
Menu TABLE → OPTN → → STAT → DIST → BINM → Bcd
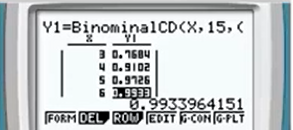
Ensuite il vous faut remplir comme suit à l'écran : BinominalCD(,,) ici on va mettre BinominalCD(,,)

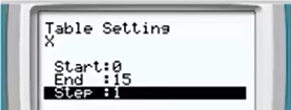
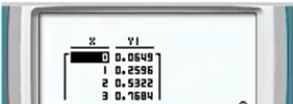
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
Question 3
Soit une variable aléatoire qui suit une loi binomiale de paramètres et . Déterminer l'intervalle de fluctuation au seuil de .
Correction
L'intervalle de fluctuation à d'une fréquence correspondant à la réalisation, sur un échantillon de taille , d'une variable aléatoire X de loi binomiale , est l'intervalle défini par :
1ère cas de figure : A l'aide d'une Texas, nous suivons la procédure comme suit :- est le plus petit entier tel que :
- est le plus petit entier tel que
Touche ou → VAR → Choisir BinomFREP puis écrire BinomFREP(,,)
Puis faire 2nde → Fenêtre puis remplir DébutTbl : et Tbl : et enfin 2nde → Graphe
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
- ce qui nous donne
- ce qui nous donne
2ème cas de figure : A l'aide d'une Casio graph , nous suivons la procédure comme suit :
Menu TABLE → OPTN → → STAT → DIST → BINM → Bcd
Ensuite il vous faut remplir comme suit à l'écran : BinominalCD(,,) ici on va mettre BinominalCD(,,) puis . Ensuite renseigné pour START : et END : et Step : puis EXE puis
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
- ce qui nous donne
- ce qui nous donne
Question 4
Soit une variable aléatoire qui suit une loi binomiale de paramètres et . Déterminer l'intervalle de fluctuation au seuil de .
Correction
L'intervalle de fluctuation à d'une fréquence correspondant à la réalisation, sur un échantillon de taille , d'une variable aléatoire X de loi binomiale , est l'intervalle défini par :
1ère cas de figure : A l'aide d'une Texas, nous suivons la procédure comme suit :- est le plus petit entier tel que :
- est le plus petit entier tel que
Touche ou → VAR → Choisir BinomFREP puis écrire BinomFREP(,,)
Puis faire 2nde → Fenêtre puis remplir DébutTbl : et Tbl : et enfin 2nde → Graphe
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
- ce qui nous donne
- ce qui nous donne
2ème cas de figure : A l'aide d'une Casio graph , nous suivons la procédure comme suit :
Menu TABLE → OPTN → → STAT → DIST → BINM → Bcd
Ensuite il vous faut remplir comme suit à l'écran : BinominalCD(,,) ici on va mettre BinominalCD(,,) puis . Ensuite renseigné pour START : et END : et Step : puis EXE puis
Apparaitra un tableau de valeur et dans la colonne , il va falloir chercher la valeur tel que et la valeur tel que
Il en résulte donc que :
- ce qui nous donne
- ce qui nous donne