Probabilités conditionnelles et indépendance
Vérifier si deux évènements sont indépendants - Exercice 5
6 min
15
On considère les évènements ; ; et associés à une expérience aléatoire modélisée par l'arbre pondéré ci-dessous :
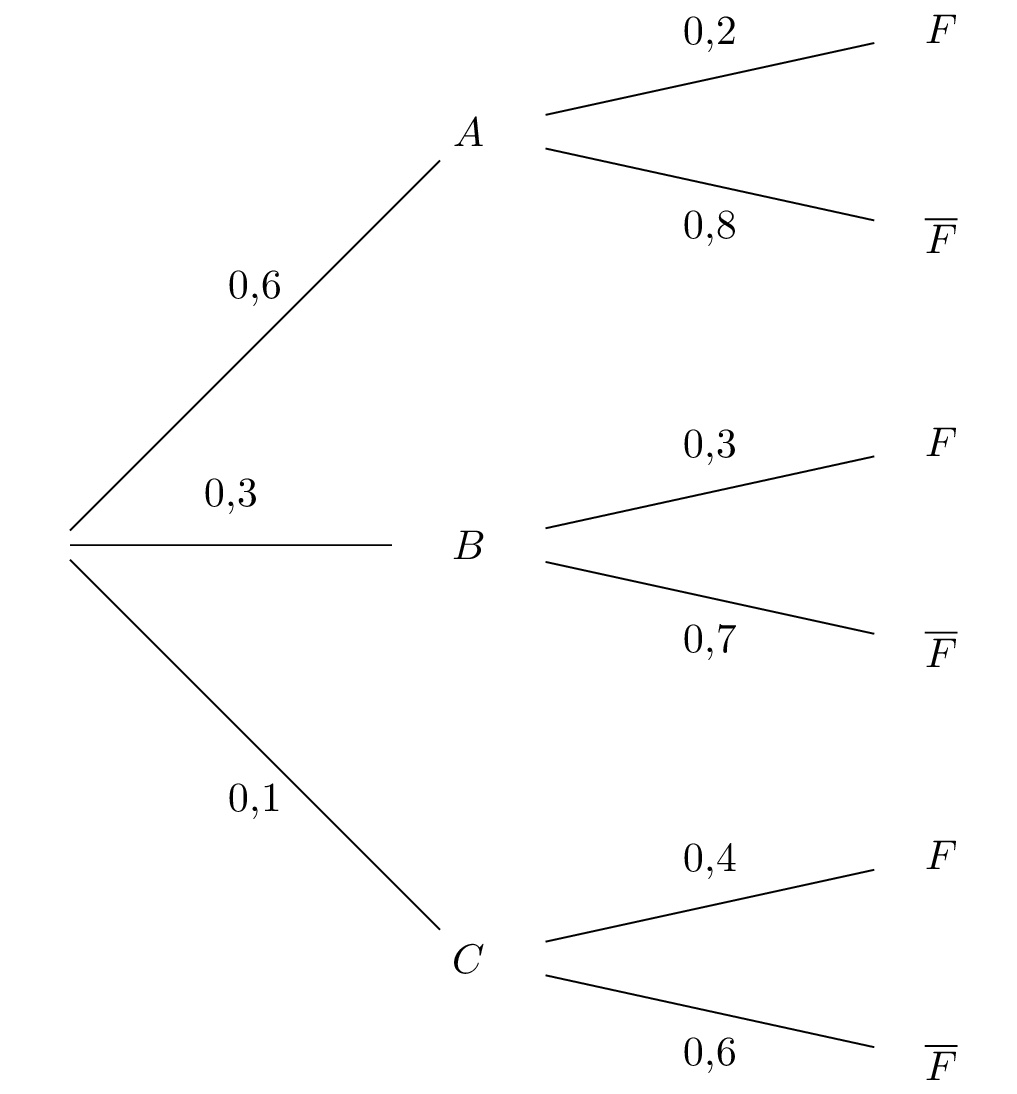
Question 1
Calculer
Correction

Ainsi :
Question 2
Calculer .
Correction

D'après la formule des probabilités totales on a :
Ainsi :
Question 3
Les évènements et sont-ils indépendants ?
Correction
- Deux événements et sont indépendants si et seulement si :
-
Les évènements et .