Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Loi de probabilités : variance et écart type - Exercice 1
15 min
20
Un jeu consiste à tirer une carte dans un jeu de cartes.
Un joueur mise € sur l'as de cœur.
Le gain du joueur est modélisé par la variable aléatoire .
Un joueur mise € sur l'as de cœur.
- Si la carte est bien l'as de cœur, le joueur reçoit €.
- Si la carte est un autre as, il reçoit €.
- Si la carte est un cœur, il reçoit un €.
- Dans tous les autres cas, il perd sa mise.
Le gain du joueur est modélisé par la variable aléatoire .
Question 1
Quelles sont les valeurs prisent par ?
Correction
Le gain du joueur est la somme reçue moins sa mise.
Ainsi, prendra les valeurs
Ainsi, prendra les valeurs
Question 2
Donner la loi de probabilité de
Correction
On va commencer par calculer les probabilités des différents cas :
(il n'y a qu'un seul as de cœur dans le jeu de cartes )
(il y a quatre as dans le jeu de cartes , mais on ne recompte pas l'as de cœur)
(il y a huit cœurs dans le jeu de cartes , mais on ne recompte pas l'as de cœur)
(ce sont toutes les cartes restantes )
On va traduire ces informations dans un tableau que l'on appellera loi de probabilité :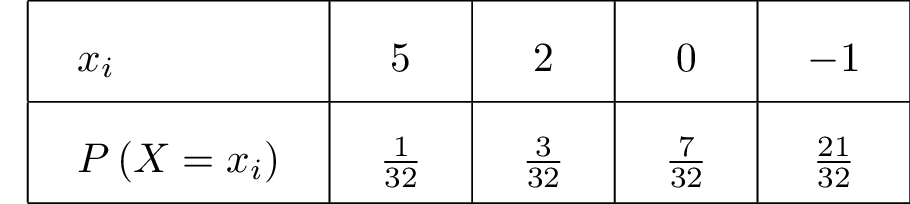
(il n'y a qu'un seul as de cœur dans le jeu de cartes )
(il y a quatre as dans le jeu de cartes , mais on ne recompte pas l'as de cœur)
(il y a huit cœurs dans le jeu de cartes , mais on ne recompte pas l'as de cœur)
(ce sont toutes les cartes restantes )
On va traduire ces informations dans un tableau que l'on appellera loi de probabilité :

Question 3
Calculer et
Le jeu est-il favorable au joueur ?
Le jeu est-il favorable au joueur ?
Correction
- On appelle l’espérance mathématique de la variable , la quantité notée définie par :
- La formule de l'écart type est obtenue après avoir calculer la variance . Les formules de la variance et de l'écart type sont données ci-dessous :

Soit
Comme l'espérance est strictement négative, le jeu est défavorable au joueur.
Ainsi :
d'où
Finalement :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.