Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 33ème partie - Exercice 1

20 min
35
Victor a téléchargé un jeu sur son téléphone.
Le but de ce jeu est d’affronter des obstacles à l’aide de personnages qui peuvent être de trois types : «Terre», «Air» ou «Feu».
Au début de chaque partie, Victor obtient de façon aléatoire un personnage d’un des trois types et peut, en cours de partie, conserver ce personnage ou changer une seule fois de type de personnage. Le jeu a été programmé de telle sorte que :
  • la probabilité que la partie débute avec un personnage de type «Terre» est 0,30,3 ;
  • la probabilité que la partie débute avec un personnage de type «Air» est 0,50,5 ;
  • si la partie débute avec un personnage de type «Terre», la probabilité que celui-ci soit conservé est 0,50,5;
  • si la partie débute avec un personnage de type «Air», la probabilité que celui-ci soit conservé est 0,40,4 ;
  • si la partie débute avec un personnage de type «Feu», la probabilité que celui-ci soit conservé est 0,90,9 .
    • On note les évènements suivants :
  • TT : la partie débute avec un personnage de type «Terre» ;
  • AA : lapartie débuteavec un personnage de type «Air» ;
  • FF : lapartie débute avec un personnage de type «Feu» ;
  • CC : Victor conserve le même personnage tout au long de la partie.
    • Question 1

    Dresser l'arbre pondéré traduisant la situation.

    Correction
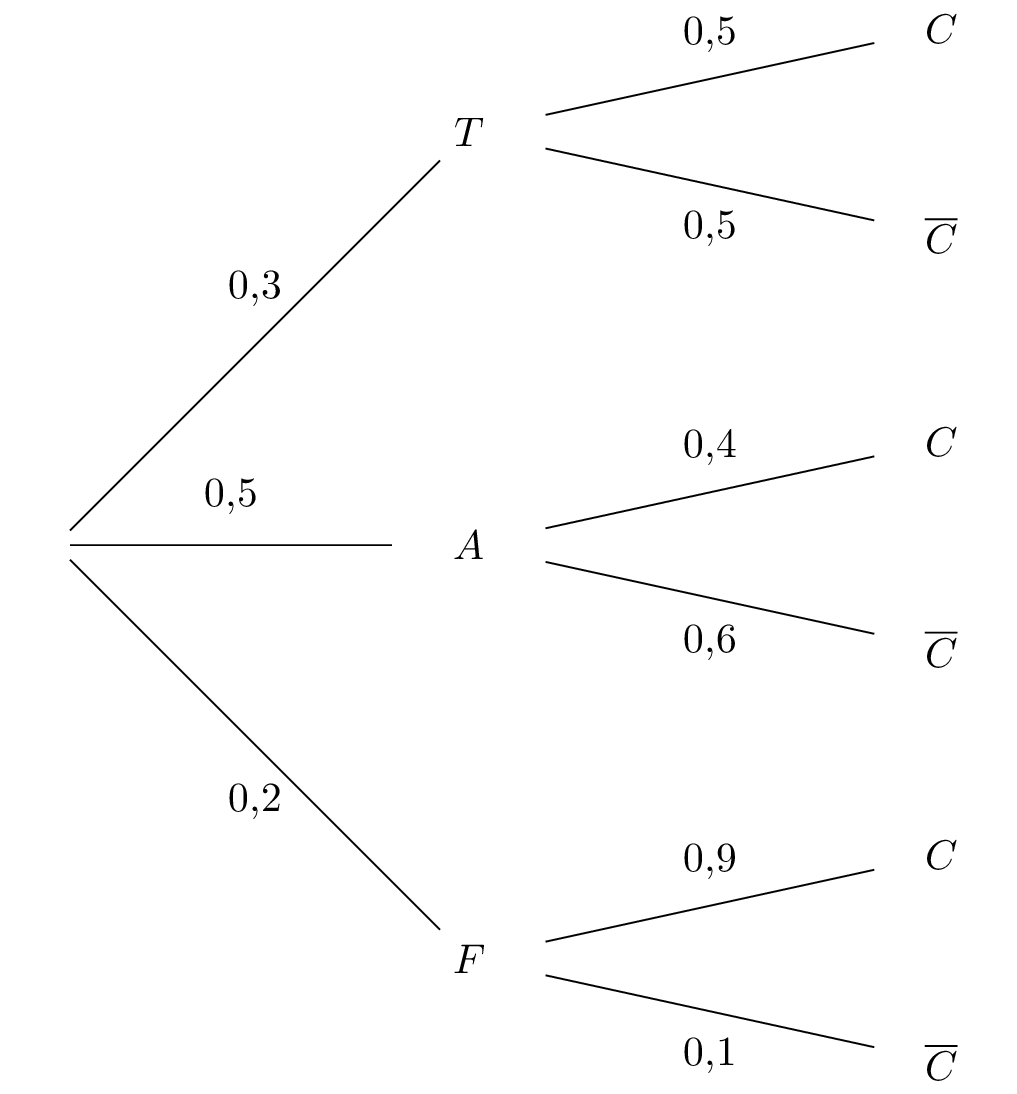
    Question 2

    Calculer la probabilité que Victor obtienne et conserve un personnage de type «Air» .

    Correction
    Victor obtient et conserve un personnage de type «Air» correspond à l’événement A∩CA\cap C.
    Il en résulte que :
    P(A∩C)=P(A)×PA(C)P\left(A\cap C\right)=P\left(A\right)\times P_{A} \left(C\right)
    P(A∩C)=0,5×0,4P\left(A\cap C\right)=0,5\times 0,4
    P(A∩C)=0,2P\left(A\cap C\right)=0,2
    Question 3

    Justifier que la probabilité que Victor conserve le personnage obtenu en début de partie est 0,530,53.

    Correction
    Les évènements TT; AA et FF forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    P(C)=P(T∩C)+P(A∩C)+P(F∩C)P\left(C\right)=P\left(T \cap C\right)+P\left(A \cap C\right)+P\left(F \cap C\right) équivaut successivement à :
    P(C)=P(T)×PT(C)+P(A)×PA(C)+P(F)×PF(C)P\left(C\right)=P\left(T\right)\times P_{T} \left(C\right)+P\left(A\right)\times P_{A} \left(C\right)+P\left(F\right)\times P_{F} \left(C\right)
    P(C)=0,3×0,5+0,5×0,4+0,2×0,9P\left(C\right)= 0,3\times 0,5+0,5\times 0,4+0,2\times 0,9
    P(C)=0,53P\left(C\right)=0,53

    Question 4

    On considère une partie au cours de laquelle Victor a conservé le personnage obtenu en début de partie. Quelle est la probabilité que ce soit un personnage de type «Air»?

    Correction
    Il s'agit ici d'une forme avec un "sachant" c'est-à-dire une probabilité conditionnelle.
    On pourrait traduire la question de la manière suivante ; sachant{\color{blue}{\text{sachant}}} que Victor a conservé le personnage en début de partie, quelle est la probabilité que ce soit un personnage de type «Air».
    • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}
    Il vient alors que :
    PC(A)=P(A∩C)P(C)P_{C} \left(A\right)=\frac{P\left(A\cap C\right)}{P\left(C\right)}
    PC(A)=P(A)×PA(C)P(C)P_{C} \left(A\right)=\frac{P\left(A\right)\times P_{A} \left(C\right)}{P\left(C\right)}
    PC(A)=0,5×0,40,53P_{C} \left(A\right)=\frac{0,5\times 0,4}{0,53} d'où :
    PC(A)≈0,38P_{C} \left(A\right)\approx 0,38

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.