Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 1

25 min
45
Une usine fabrique des étuis en cuir pour téléphone mobile. Chaque étui produit est soumis à deux contrôles :
  • Un contrôle de qualité de finition : l’étui ne doit pas présenter de défaut définition
  • Un contrôle de solidité : l'étui est exclu de la vente s'il n'est pas solide.
    • Il s'avère, à la suite d'un grand nombre de vérifications, que :
  • 9494% des étuis sont sans défaut de fabrication; parmi les étuis qui sont sans défaut de définition, 9696% réussissent le test de solidité.
  • 22% des étuis ne satisfont à aucun des deux contrôles.
    • On prend au hasard un étui parmi les étuis produits. On note :
  • FF l'évènement : " l'étui est sans défaut de finition "
  • SS l'évènement : " l'étui réussit le rest de solidité "
    • Question 1

    En utilisant l'énoncé, préciser : P(F)P\left(F\right) ; PF(S)P_{F} \left(S\right) et P(F‾∩S‾)P\left(\overline{F}\cap \overline{S}\right)

    Correction
    D'après l'énoncé, on a :
  • P(F)=0,94P\left(F\right)=0,94
  • PF(S)=0,96P_{F} \left(S\right)=0,96
  • P(F‾∩S‾)=0,02P\left(\overline{F}\cap \overline{S}\right)=0,02
    • Question 2

    Démontrer que : PF‾(S‾)=13P_{\overline{F}} \left(\overline{S}\right)=\frac{1}{3}

    Correction
    Il s'agit d'une probabilité conditionnelle. Il vient alors :
    PF‾(S‾)=P(F‾∩S‾)P(F‾)P_{\overline{F}} \left(\overline{S}\right)=\frac{P\left(\overline{F}\cap \overline{S}\right)}{P\left(\overline{F}\right)}
    PF‾(S‾)=0,020,06P_{\overline{F}} \left(\overline{S}\right)=\frac{0,02}{0,06}
    Ainsi :
    PF‾(S‾)=13P_{\overline{F}} \left(\overline{S}\right)=\frac{1}{3}
    Question 3

    Donner au complet l'arbre pondéré correspondant à cette situation.

    Correction
    On représente la situation par un arbre pondéré :
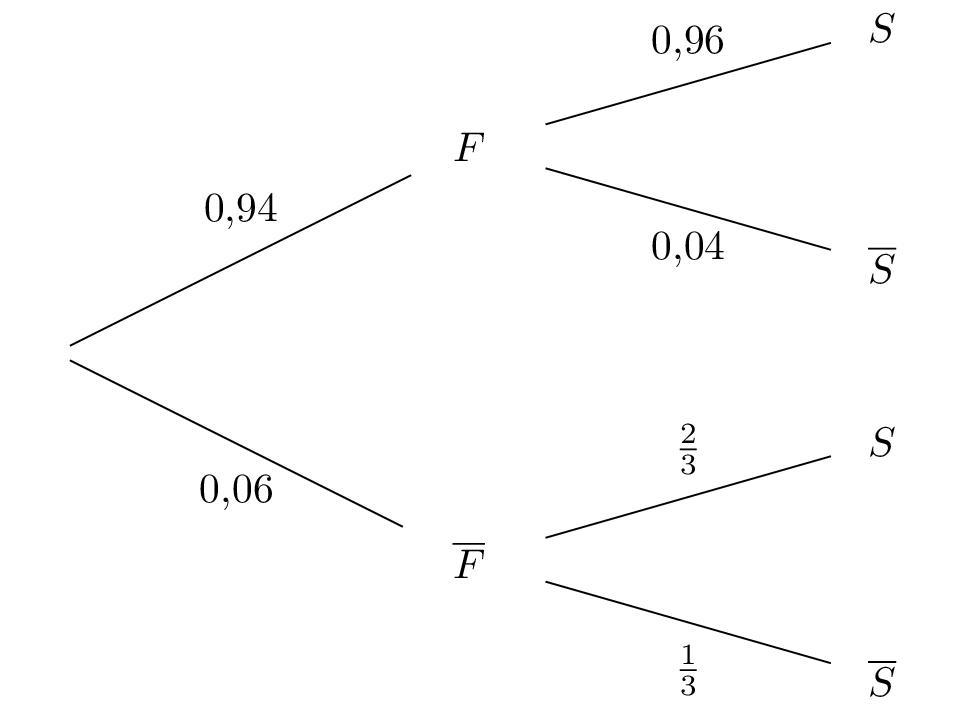
    Question 4

    Démontrer que P(S)=0,9424P\left(S\right)=0,9424

    Correction
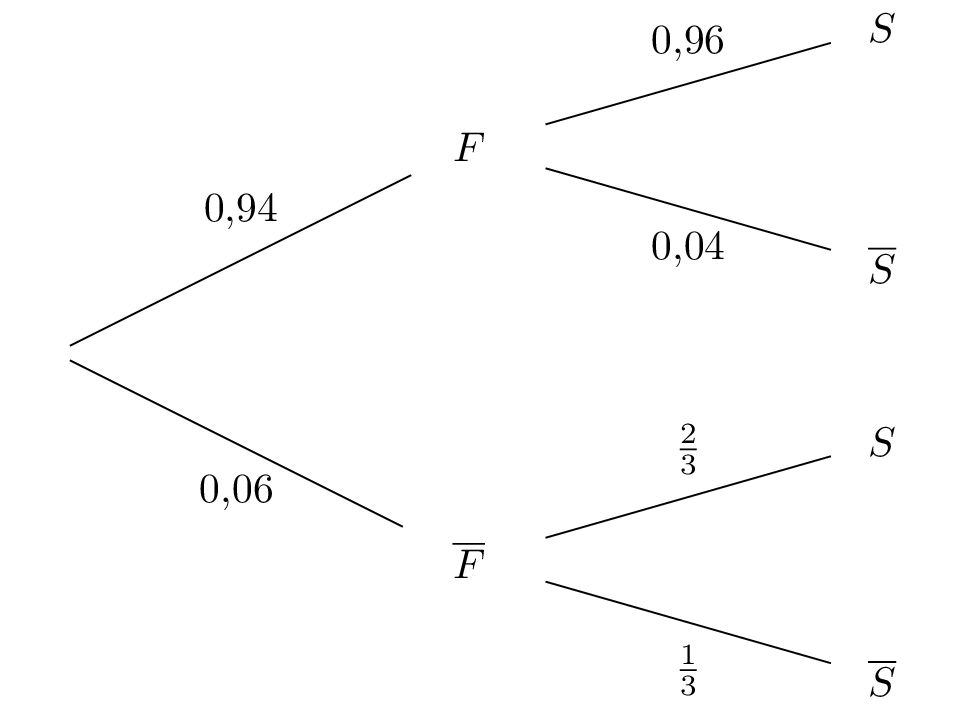
    Les évènements FF et F‾\overline{F} forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    P(S)=P(F∩S)+P(F‾∩S)P\left(S\right)=P\left(F \cap S\right)+P\left(\overline{F} \cap S\right) équivaut successivement à :
    P(S)=P(F)×PF(S)+P(F‾)×PF‾(S)P\left(S\right)=P\left(F\right)\times P_{F} \left(S\right)+P\left(\overline{F}\right)\times P_{\overline{F}} \left(S\right)
    P(S)=0,94×0,96+0,06×23P\left(S\right)=0,94\times0,96 + 0,06\times \frac{2}{3}
    P(S)=0,9424P\left(S\right)=0,9424
    Question 5

    Un étui a réussi le test de solidité. Calculer la probabilité qu'il soit sans défaut de finition. On donnera le résultat arrondi au dix-millième.

    Correction
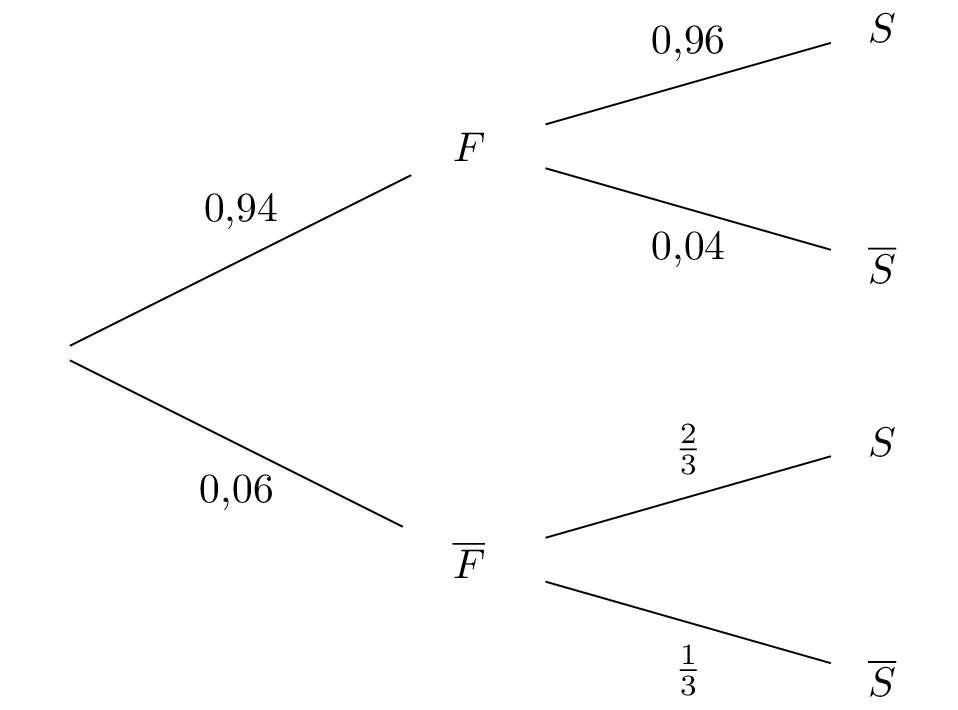
    On cherche cette fois à calculer une probabilité conditionnelle. On pourrait traduire la question de la manière suivante ; sachant{\color{blue}{\text{sachant}}} que l'étui a réussi le test de solidité, quelle est la probabilité qu'il soit sans défaut de finition.
    Ainsi :
    PS(F)=P(F∩S)P(S)P_{S} \left(F\right)=\frac{P\left(F\cap S\right)}{P\left(S\right)}
    PS(F)=0,94×0,960,9424P_{S} \left(F\right)=\frac{0,94\times0,96}{0,9424}
    Ainsi :
    PS(F)≈0,9576P_{S} \left(F\right)\approx0,9576

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.