Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
20 min
35
Une jardinerie vend de jeunes plants d’arbres qui proviennent de trois horticulteurs : % des plants proviennent de l’horticulteur , % de l’horticulteur et le reste de l’horticulteur . Chaque horticulteur livre deux catégories d’arbres : des conifères et des arbres à feuilles.
La livraison de l’horticulteur comporte % de conifères alors que celle de l’horticulteur n’en comporte que % et celle de l’horticulteur seulement %.
Le gérant de la jardinerie choisit un arbre au hasard dans son stock. On envisage les événements suivants :
- : " l'arbre choisi a été acheté chez l'horticulteur ".
- : " l'arbre choisi a été acheté chez l'horticulteur ".
- : " l'arbre choisi a été acheté chez l'horticulteur ".
- : " l'arbre choisi est un conifère".
- : " l'arbre choisi est un feuillu".
Question 1
Construire un arbre pondéré traduisant la situation.
Correction
Puisque le choix de l’arbre se fait au hasard dans le stock de la jardinerie, on assimile les proportions données à des probabilités.
L'arbre pondéré traduisant la situation est :
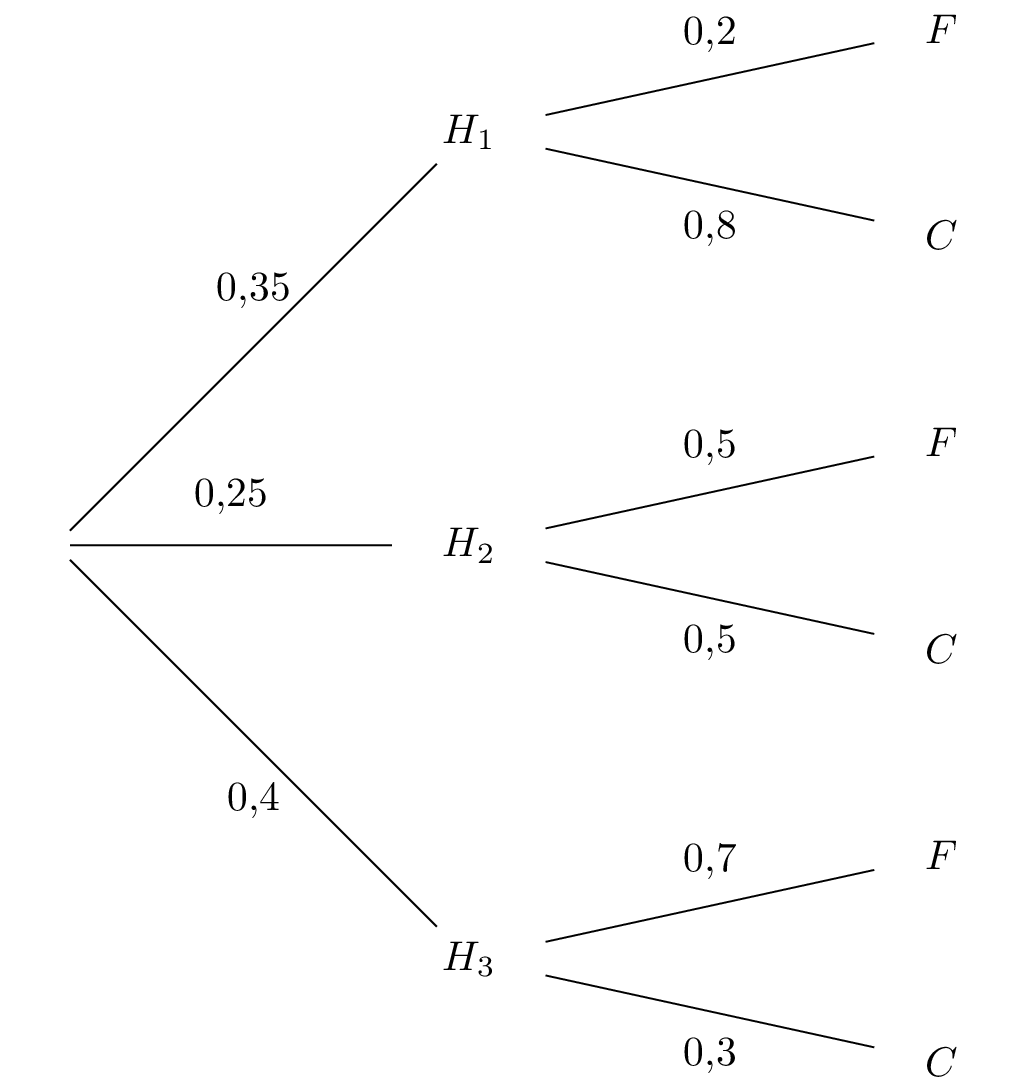
L'arbre pondéré traduisant la situation est :

Question 2
Calculer la probabilité que l’arbre choisi soit un conifère acheté chez l’horticulteur .
Correction
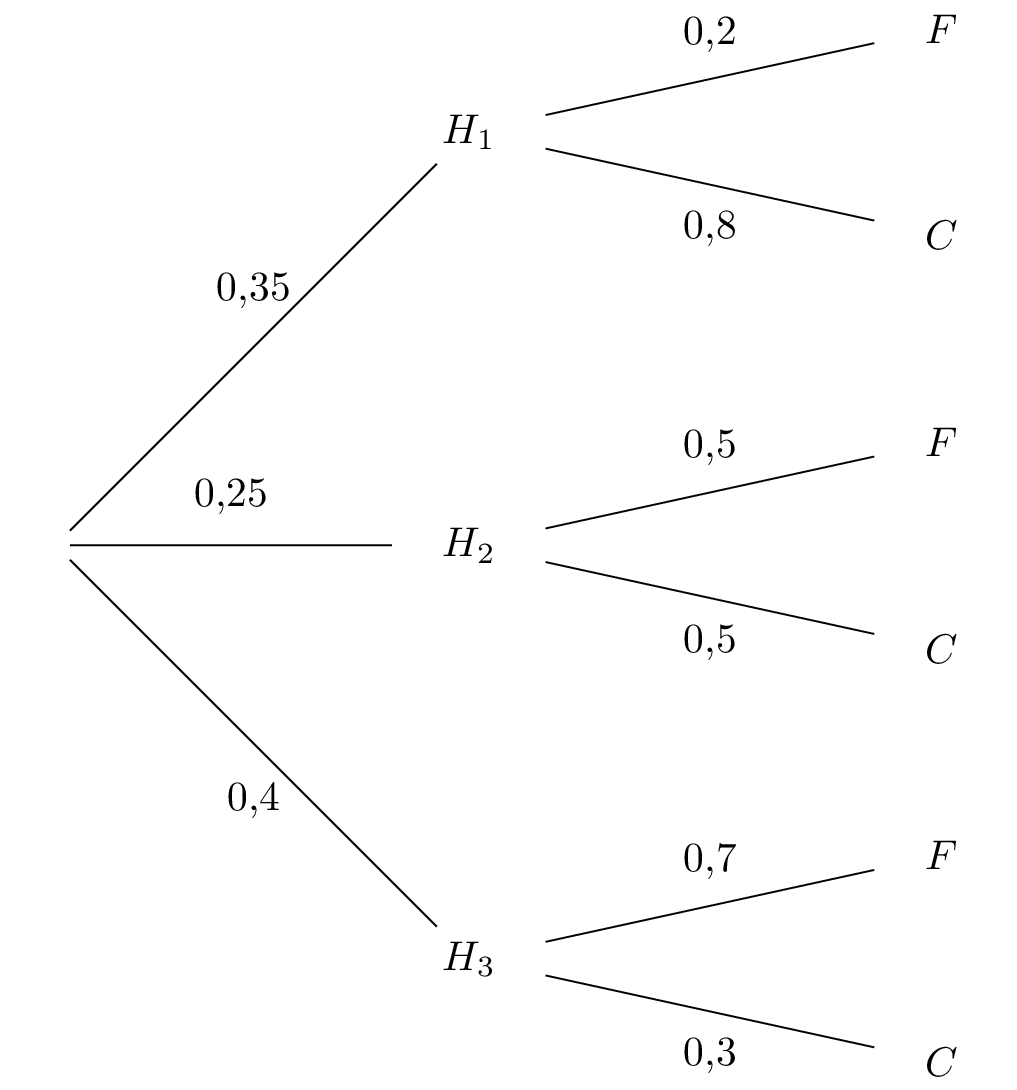
Il en résulte que :
D'où :
Question 3
Justifier que la probabilité de l’évènement est égale à .
Correction
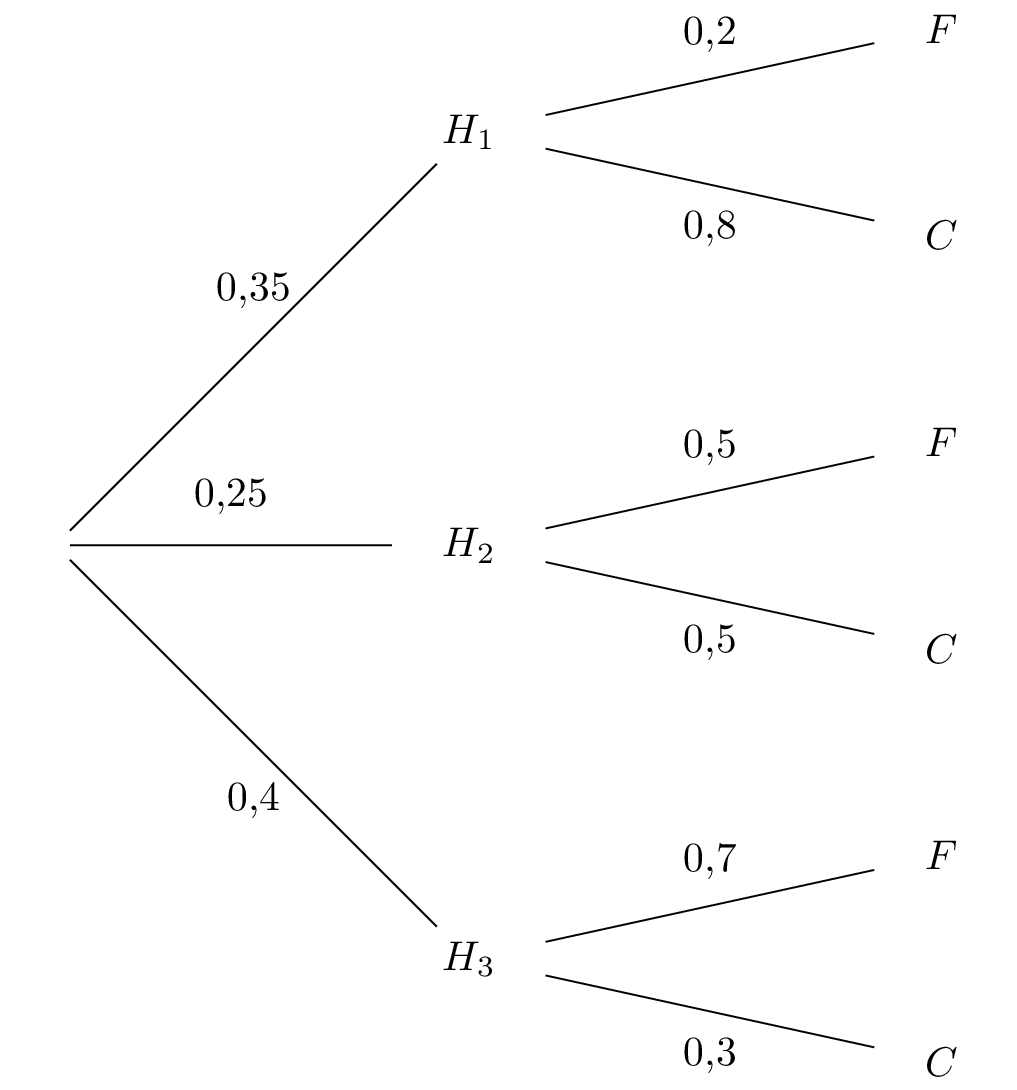
D'après la formule des probabilités totales, on a :
équivaut successivement à :
Ainsi :
Question 4
L’arbre choisi est un conifère.
Quelle est la probabilité qu’il ait été acheté chez l’horticulteur ? On arrondira à .
Quelle est la probabilité qu’il ait été acheté chez l’horticulteur ? On arrondira à .
Correction
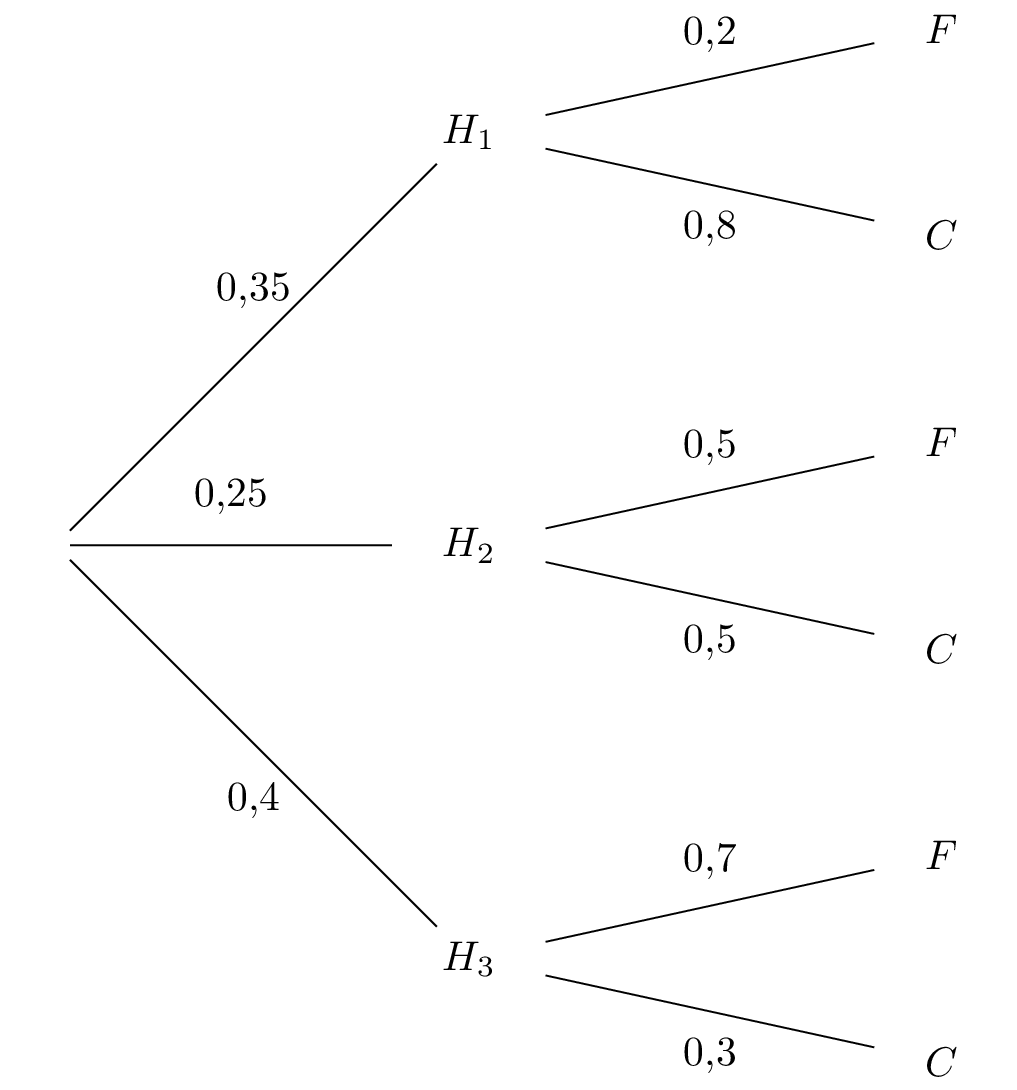
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.