Probabilités conditionnelles et indépendance

Deux premiers exemples de sujets bilan - Exercice 2

20 min
40
Une entreprise a fabriqué en un mois 15001 500 chaudières, dont 900900 chaudières à cheminée et 600600 chaudières à ventouse.
On a constaté, dans ce lot, que :
  • 1%1\% des chaudières à cheminées ont un défaut
  • 6%6\% des chaudières à ventouses ont un défaut.
    • On prélève au hasard le numéro de série d’une chaudière de la production de ce mois.
    On considère les évènements suivants :
  • CC : « Le numéro de série est celui d’une chaudière à cheminée »
  • VV : « Le numéro de série est celui d’une chaudière à ventouse »
  • DD : « Le numéro de série est celui d’une chaudière défectueuse »
    • Question 1

    Dresser l'arbre pondéré traduisant la situation .

    Correction
    D'après l'énoncé, nous savons que :
    P(C)=9001500=0,6P\left(C\right)=\frac{900}{1500}=0,6
    P(V)=6001500=0,4P\left(V\right)=\frac{600}{1500}=0,4
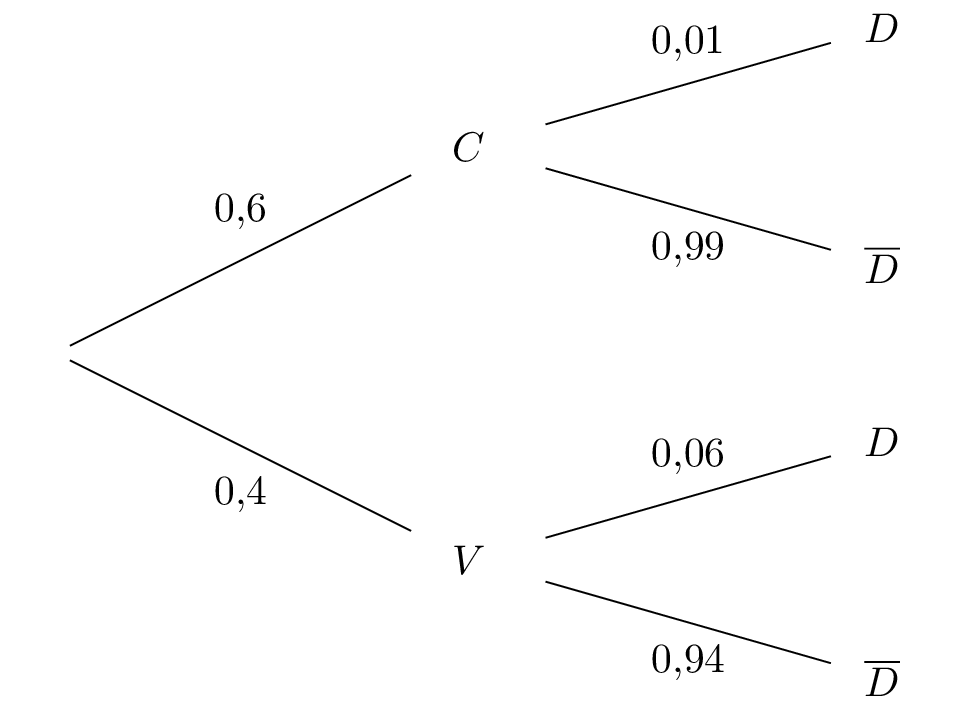
    Il en résulte donc que :
    Question 2

    Calculer la probabilité que le numéro de série est celui d’une chaudière à ventouse défectueuse.

    Correction
    La probabilité que le numéro de série est celui d’une chaudière à ventouse défectueuse.se traduit par P(V∩D)P\left(V\cap D\right)
    On calcule alors :
    P(V∩D)=P(V)×PV(D)P\left(V\cap D\right)=P\left(V\right)\times P_{V} \left(D\right)
    P(V∩D)=0,4×0,06P\left(V\cap D\right)=0,4\times 0,06
    Ainsi :
    P(V∩D)=0,024P\left(V\cap D\right)=0,024

    La probabilité que le numéro de série est celui d’une chaudière à ventouse défectueuse est alors de 0,0240,024.
    Question 3

    Déterminer la probabilité de l'évènement le numéro de série est celui d’une chaudière défectueuse.

    Correction
    CC et VV forment une partition de l'univers.
    D'après la formule des probabilités totales on a :
    P(D)=P(C∩D)+P(V∩D)P\left(D\right)=P\left(C\cap D\right)+P\left(V\cap D\right)
    P(D)=P(C)×PC(D)+P(V)×PV(D)P\left(D\right)=P\left(C\right)\times P_{C} \left(D\right)+P\left(V\right)\times P_{V} \left(D\right)
    P(D)=0,6×0,01+0,4×0,06P\left(D\right)=0,6\times0,01+0,4\times0,06
    P(D)=0,006+0,024P\left(D\right)=0,006+0,024
    Ainsi :
    P(D)=0,03P\left(D\right)=0,03
    Question 4

    Le numéro de série est celui d'une chaudière défectueuse. Quelle est la probabilité que le numéro de série soit celui d'une chaudière à cheminée ?

    Correction
    Il s'agit ici d'une forme avec un "sachant" c'est-à-dire une probabilité conditionnelle.
    On pourrait traduire la question de la manière suivante ; sachant{\color{blue}{\text{sachant}}} que le numéro de série est celui d'une chaudière défectueuse , quelle est la probabilité que le numéro de série soit celui d'une chaudière à cheminée ?
    • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}
    On souhaite calculer PD(C)P_{D} \left(C\right), il vient alors que :
    PD(C)=P(C∩D)P(D)P_{D} \left(C\right)=\frac{P\left(C\cap D\right)}{P\left(D\right)}
    PD(C)=P(C)×PC(D)P(D)P_{D} \left(C\right)=\frac{P\left(C\right)\times P_{C} \left(D\right)}{P\left(D\right)}
    PD(C)=0,6×0,010,03P_{D} \left(C\right)=\frac{0,6\times 0,01}{0,03} d'où :
    PD(C)=0,2P_{D} \left(C\right)=0,2
    Question 5

    Les évènements DD et VV sont-ils indépendants ?

    Correction
      Deux événements AA et BB sont indépendants si et seulement si :
    • P(A∩B)=P(A)×P(B)P\left(A\cap B\right)=P\left(A\right) \times P\left(B\right)
    D'après les questions précédentes, nous savons que : P(D)=0,03P\left(D\right)=0,03 ; P(V)=0,4P\left(V\right)=0,4 et P(V∩D)=0,024P\left(V\cap D\right)=0,024
    D’une part :\red{\text{D'une part :}} P(V)×P(D)=0,4×0,03P\left(V\right) \times P\left(D\right)=0,4 \times 0,03 d'où P(V)×P(D)=0,012P\left(V\right) \times P\left(D\right)=0,012
    D’autre part :\red{\text{D'autre part :}} P(V∩D)=0,024P\left(V\cap D\right)=0,024
    Finalement :\purple{\text{Finalement :}}
    P(V∩D)≠P(V)×P(D)P\left(V\cap D\right)\ne P\left(V\right) \times P\left(D\right)
    Les évènements VV et DD ne sont pas indeˊpendants\text{\red{ne sont pas indépendants}}.