Probabilités conditionnelles et indépendance

D'autres sujets bilan - Exercice 2

15 min
30
Une chaîne de salons de coiffure propose à ses clients qui viennent pour une coupe deux prestations supplémentaires cumulables :
  • une coloration naturelle à base de plantes appelée « couleur-soin »,
  • des mèches blondes pour donner du relief à la chevelure, appelées « effet coup de soleil ».
    • Il apparaît que 40%40\% des clients demandent une « couleur-soin ».
    Parmi ceux qui ne veulent pas de « couleur soin », 30%30\% des clients demandent un « effet coup de soleil ».
    Par ailleurs, 24%24\% des clients demandent une « couleur soin » et un « effet coup de soleil ».
    On interroge un client au hasard.
    On notera CC l’évènement « Le client souhaite une "couleur-soin." ».
    On notera EE l’évènement « Le client souhaite un "effet coup de soleil." ».
    Question 1

    Dresser l'arbre pondéré traduisant la situation.

    Correction
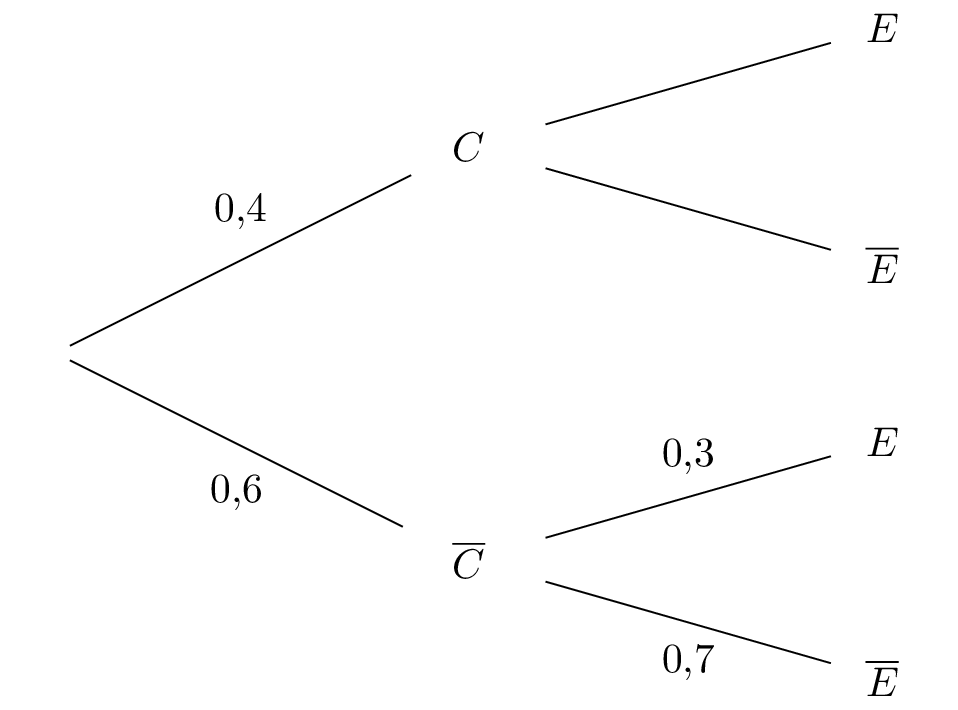
    Question 2

    Calculer la probabilité que le client ne souhaite ni une « couleur-soin », ni un « effet coup de soleil ».

    Correction
    La probabilité que le client ne souhaite ni une « couleur-soin », ni un « effet coup de soleil » se traduit par P(C‾∩E‾)P\left(\overline{C}\cap \overline{E}\right).
    On calcule alors :
    P(C‾∩E‾)=P(C‾)×PC‾(E‾)P\left(\overline{C}\cap \overline{E}\right)=P\left(\overline{C}\right)\times P_{\overline{C}} \left(\overline{E}\right)
    P(C‾∩E‾)=0,6×0,7P\left(\overline{C}\cap \overline{E}\right)=0,6\times 0,7
    Ainsi :
    P(C‾∩E‾)=0,42P\left(\overline{C}\cap \overline{E}\right)=0,42

    Question 3

    Montrer que la probabilité de l’évènement EE est égale à 0,420,42.

    Correction
    D'après l'énoncé, nous savons que 24%24\% des clients demandent une « couleur soin » et un « effet coup de soleil ». Cela se traduit par : P(C∩E)=0,24P\left(C\cap E\right)=0,24
    CC et C‾\overline{C} forment une partition de l'univers.
    D'après la formule des probabilités totales on a :
    P(E)=P(C∩E)+P(C‾∩E)P\left(E\right)=P\left(C\cap E\right)+P\left(\overline{C}\cap E\right)
    Soit : P(E)=0,24+0,6×0,3P\left(E\right)=0,24+0,6\times0,3
    P(E)=0,24+0,18P\left(E\right)=0,24+0,18
    Ainsi :
    P(E)=0,42P\left(E\right)=0,42
    Question 4

    Les évènements CC et EE sont-ils indépendants ?

    Correction
      Deux événements AA et BB sont indépendants si et seulement si :
    • P(A∩B)=P(A)×P(B)P\left(A\cap B\right)=P\left(A\right) \times P\left(B\right)
    D'après les questions précédentes, nous savons que : P(C)=0,4P\left(C\right)=0,4 ; P(E)=0,42P\left(E\right)=0,42 et P(C∩E)=0,42P\left(C\cap E\right)=0,42
    D’une part :\red{\text{D'une part :}} P(C)×P(E)=0,4×0,42P\left(C\right) \times P\left(E\right)=0,4 \times 0,42 d'où P(C)×P(E)=0,168P\left(C\right) \times P\left(E\right)=0,168
    D’autre part :\red{\text{D'autre part :}} P(C∩E)=0,42P\left(C\cap E\right)=0,42
    Finalement :\purple{\text{Finalement :}}
    P(C∩E)≠P(C)×P(E)P\left(C\cap E\right)\ne P\left(C\right) \times P\left(E\right)
    Les évènements CC et EE ne sont pas indeˊpendants\text{\red{ne sont pas indépendants}}.