Premières notions sur les suites numériques

Comment représenter graphiquement les termes d'une suite récurrente - Exercice 2

5 min
15
COMPETENCE‾  :  Repreˊsenter{\color{red}\underline{COMPETENCE}\;:\;Représenter}
(un)\left(u_{n}\right) est la suite définie par : {u0=65un+1=(un)2\left\{\begin{array}{ccc} {u_{0} } & {=} & {\frac{6}{5}} \\ {u_{n+1} } & {=} & {\left(u_{n}\right)^{2}} \end{array}\right.
Dans le plan muni d’un repère orthogonal, on trace la droite d’équation y=xy = x et la courbe Cf\mathscr{C_{f}} représentative de la fonction ff définie pour tout réel xx positif par : f(x)=x2f\left(x\right)=x^{2}
Question 1

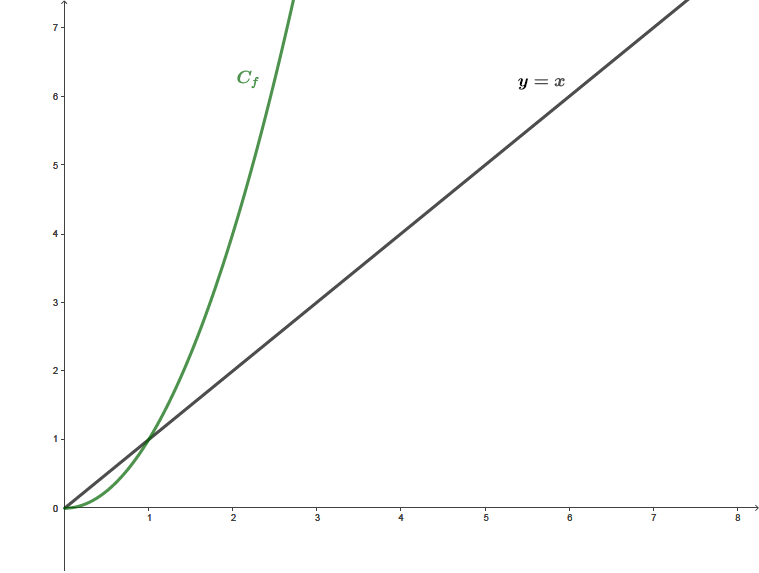
Placer sur l'axe des abscisses les termes u0u_{0}, u1u_{1}, u2u_{2} et u3u_{3} sur la représentation graphique ci-dessus.

Correction
  • On place u0u_{0} sur l'axe des abscisses. Nous pouvons donner des coordonnées à ce point sous la forme (u0;0)\left(u_{0} ;0\right)
  • Cherchons ensuite le point d'ordonnée f(u0)f\left(u_{0}\right), on l'obtient en traçant une droite verticale passant par u0u_{0} et en cherchant son intersection avec la courbe Cf\mathscr{C_{f}}. Ce point a comme ordonnée f(u0)f\left(u_{0}\right), ce qui correspond à u1u_{1} , puisque u1=f(u0)u_{1} = f\left(u_{0}\right).
  • Projetons, ensuite, horizontalement le point de coordonnées (u0;u1)\left(u_{0} ;u_{1}\right) sur la droite y=xy=x pour obtenir le point de coordonnées (u1;u1)\left(u_{1} ;u_{1}\right), une projection verticale permet ensuite de reporter le point (u1;0)\left(u_{1} ;0\right) sur l'axe des abscisses.
  • Faire de même pour obtenir u2u_{2} puis u3u_{3} et ainsi de suite.
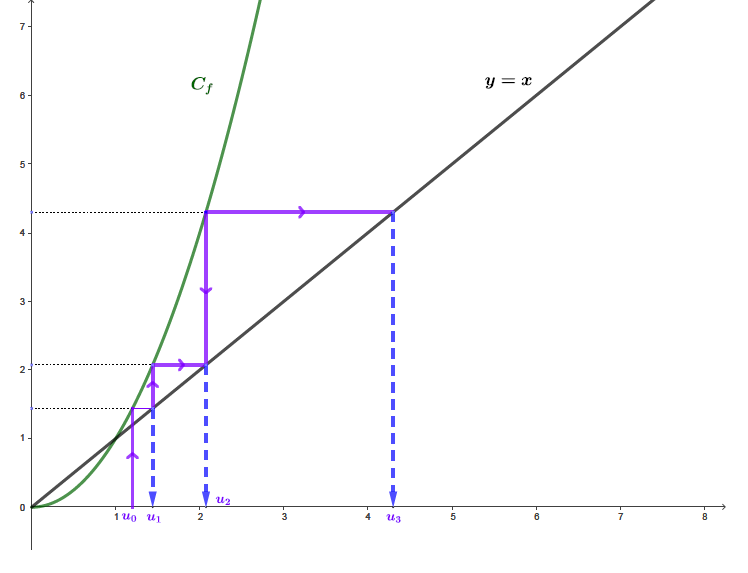
    • Question 2

    Conjecturer la variation de la suite (un)\left(u_{n}\right) .

    Correction
    D'après la question 11, nous savons que :
    On observe graphiquement que : u0<u1<u2<u3u_{0}<u_{1}<u_{2}<u_{3}.
    Autrement dit, nous conjecturons que un+1≥unu_{n+1}\ge u_{n} c'est à dire un+1−un≥0u_{n+1}-u_{n}\ge 0 .
    Nous pouvons conjecturer que la suite est (un)\left(u_{n}\right) croissante.
    Question 3

    Conjecturer la limite de la suite (un)\left(u_{n}\right) .

    Correction
    D'après la question 11, nous savons que :
    Les coordonnées du point d’intersection de Cf\mathscr{C_{f}} et y=xy=x représente une limite pour la suite (un)\left(u_{n}\right) . Cependant, la suite (un) \left(u_{n}\right) est croissante, les valeurs de la suite (un)\left(u_{n}\right) s'éloigne de plus en plus du point d'intersection entre Cf\mathscr{C_{f}} et y=xy=x .
    Avec le graphique, on conjecture que la limite serait approximativement +∞+\infty . On dit que la suite (un)\left(u_{n}\right) est divergente.