Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Droites parallèles - Exercice 2
12 min
20
Question 1
Trouver une équation de la droite passant par le point et parallèle à la droite d'équation .
Correction
On sait que deux droites sont parallèles si leurs vecteurs directeurs respectifs sont colinéaires.
Soit un vecteur de la droite .
Comme les droites et sont parallèles alors on choisit un vecteur directeur de identique à celui de .
Ainsi les deux vecteurs directeurs seront bien colinéaires.
On note un vecteur de la droite .
Ainsi l'équation cartésienne de est : .
Or le point appartient à la droite , donc les coordonnées du point vérifie
Il vient alors que :
Finalement, l'équation cartésienne de la droite parallèle à et passant par est :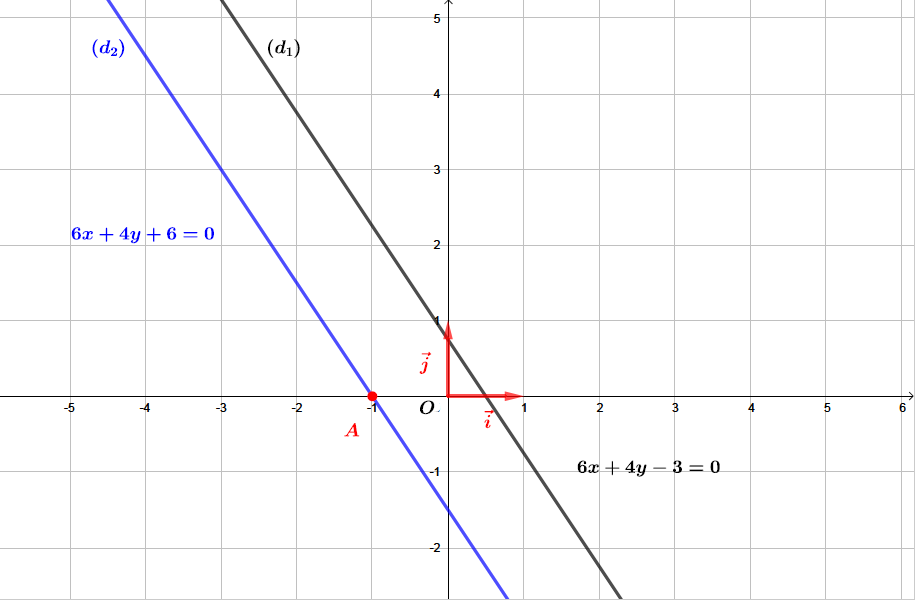
Soit un vecteur de la droite .
Comme les droites et sont parallèles alors on choisit un vecteur directeur de identique à celui de .
Ainsi les deux vecteurs directeurs seront bien colinéaires.
On note un vecteur de la droite .
Nous aurions pu prendre un autre vecteur directeur pour tant que et sont colinéaires.
Par exemple peut également convenir.
Nous avons donc choisi comme vecteur de la droite .Par exemple peut également convenir.
Ainsi l'équation cartésienne de est : .
Or le point appartient à la droite , donc les coordonnées du point vérifie
Il vient alors que :
Finalement, l'équation cartésienne de la droite parallèle à et passant par est :

Question 2
Trouver une équation de la droite passant par le point et parallèle à la droite d'équation .
Correction
On sait que deux droites sont parallèles si leurs vecteurs directeurs respectifs sont colinéaires.
Soit un vecteur de la droite .
Comme les droites et sont parallèles alors on choisit un vecteur directeur de identique à celui de .
Ainsi les deux vecteurs directeurs seront bien colinéaires.
On note un vecteur de la droite .
Ainsi l'équation cartésienne de est : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite parallèle à et passant par est : .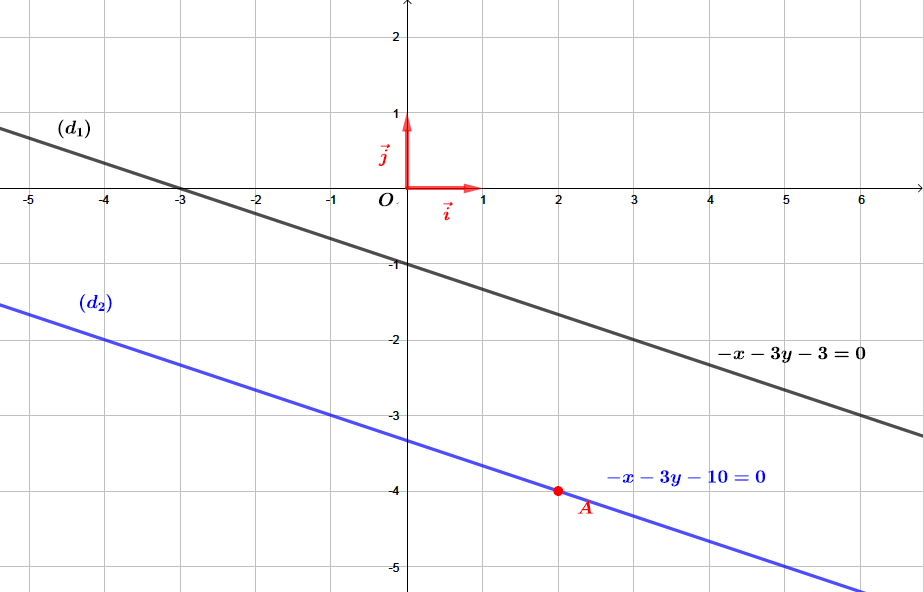
Soit un vecteur de la droite .
Comme les droites et sont parallèles alors on choisit un vecteur directeur de identique à celui de .
Ainsi les deux vecteurs directeurs seront bien colinéaires.
On note un vecteur de la droite .
Nous aurions pu prendre un autre vecteur directeur pour tant que et sont colinéaires.
Par exemple peut également convenir.
Nous avons donc choisi comme vecteur de la droite .Par exemple peut également convenir.
Ainsi l'équation cartésienne de est : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite parallèle à et passant par est : .

Question 3
Trouver une équation de la droite passant par le point et parallèle à la droite d'équation .
Correction
On sait que deux droites sont parallèles si leurs vecteurs directeurs respectifs sont colinéaires.
Soit un vecteur de la droite .
Comme les droites et sont parallèles alors on choisit un vecteur directeur de identique à celui de .
Ainsi les deux vecteurs directeurs seront bien colinéaires.
On note un vecteur de la droite .
Ainsi l'équation cartésienne de est : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite parallèle à et passant par est : .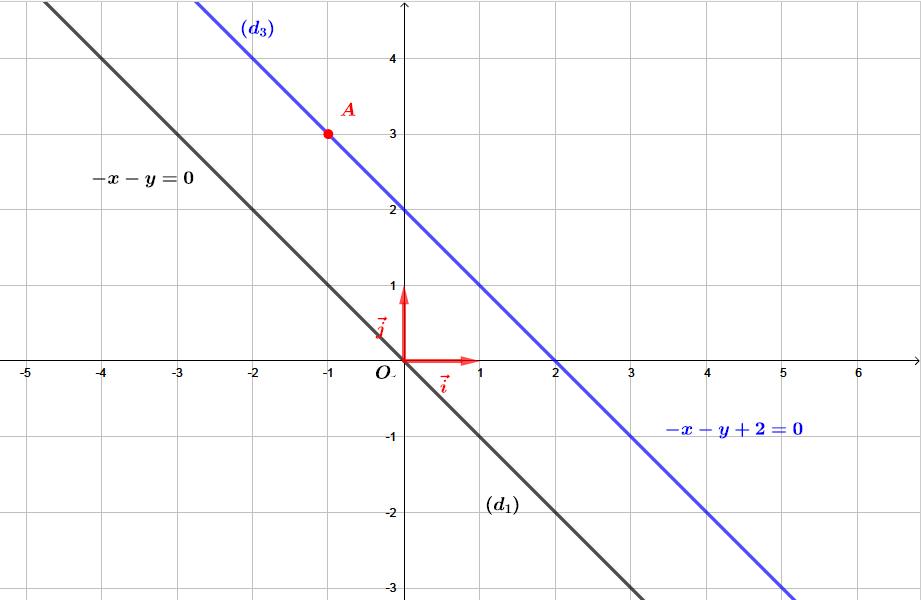
Soit un vecteur de la droite .
Comme les droites et sont parallèles alors on choisit un vecteur directeur de identique à celui de .
Ainsi les deux vecteurs directeurs seront bien colinéaires.
On note un vecteur de la droite .
Nous aurions pu prendre un autre vecteur directeur pour tant que et sont colinéaires.
Par exemple peut également convenir.
Nous avons donc choisi comme vecteur de la droite .Par exemple peut également convenir.
Ainsi l'équation cartésienne de est : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite parallèle à et passant par est : .

Question 4
Pour quelle valeur du paramètre la droite d'équation est-elle parallèle à la droite d'équation .
Correction
Soit un vecteur de la droite .
Soit un vecteur de la droite .
Pour que les droites et soient parallèles, il faut que leurs vecteurs directeurs respectifs soient colinéaires.
Ainsi :
Si alors les droites et sont bien parallèles.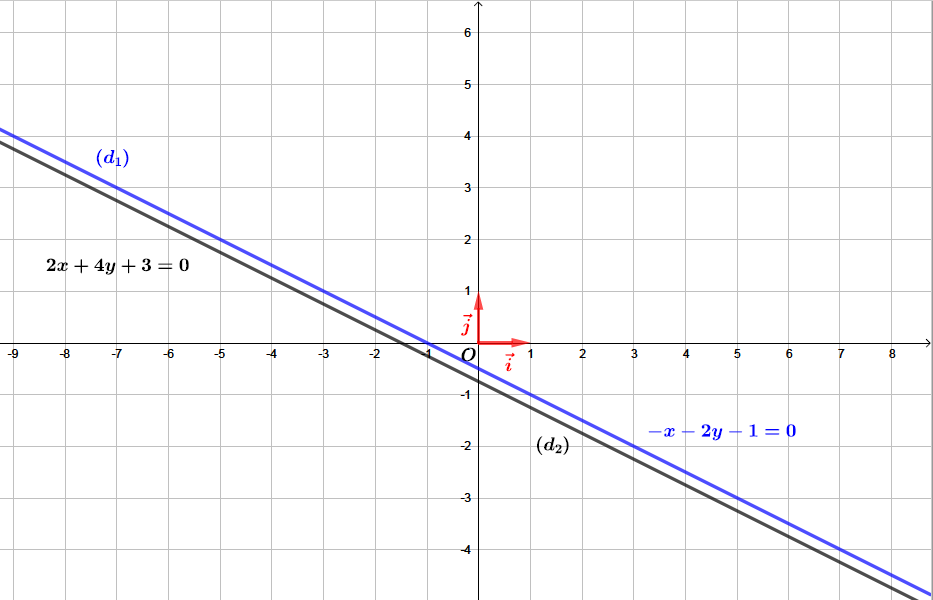
Soit un vecteur de la droite .
Pour que les droites et soient parallèles, il faut que leurs vecteurs directeurs respectifs soient colinéaires.
Ainsi :
Si alors les droites et sont bien parallèles.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.