Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

LES SUITES : Corrigé QCM Sujet 2 de voie générale - enseignement de spécialité mathématiques - Exercice 1

30 min
50
En 20202020, une ville comptait 1010 000000 habitants.
On modélise l'évolution du nombre d'habitants de cette ville par la suite (un)\left(u_n\right) définie ainsi :
{un+1=1,08un−300,n∈Nu0=10000;\left\{\begin{array}{c}u_{n+1}=1,08 u_n-300, n \in \mathbb{N} \\u_0=10000\end{array} ;\right.
où unu_n représente le nombre d'habitants pour l'année 2020+n2020+n.
Aides au calcul
10000−3750=6250;1,08×4050=4374;40501,08=3750;3750×1,08=4050.\begin{aligned} & 10000-3750=6250 ; \\ & 1,08 \times 4050=4374 ; \\ & \frac{4050}{1,08}=3750 ; \\ & 3750 \times 1,08=4050 .\end{aligned}
Question 1

Indiquer ce que représente u1u_1 et calculer sa valeur.

Correction
Nous savons que un+1=1,08un−300u_{n+1}=1,08 u_n-300 et u0=10000u_0=10000.
Il en résulte donc que :
u0+1=1,08u0−300u_{0+1}=1,08 u_0-300
u1=1,08×10000−300u_{1}=1,08\times 10000-300
Ainsi :
u1=10u_{1}=10 500500

Or unu_n représente le nombre d'habitants pour l'année 2020+n2020+n
Donc u1u_1 représente le nombre d'habitants pour l'année 2020+12020+1 c'est à dire 20212021.
Question 2

On considère la suite (vn)\left(v_n\right) définie pour tout entier naturel nn par vn=un−3750v_n=u_n-3750.
Déterminer v0v_0.

Correction
Comme vn=un−3750v_n=u_n-3750 alors
v0=u0−3750v_0=u_0-3750
v0=10000−3750v_0=10000-3750
D'où :
v0=6250v_0=6250
Question 3

Démontrer que pour tout entier naturel nn, on a vn+1=1,08vnv_{n+1}=1,08 v_n.

Correction
Nous savons que pour tout entier naturel nn, on a :
vn=un−3750v_n=u_n-3750
On va écrire maintenant l'expression au rang n+1n+1 , il vient alors que :
vn+1=un+1−3750v_{n+1} =u_{n+1} -3750 . On remplace l'expression de un+1u_{n+1} par un+1=1,08un−300u_{n+1}=1,08 u_n-300.
vn+1=1,08un−300−3750v_{n+1} =1,08 u_n-300-3750
vn+1=1,08un−4050v_{n+1} =1,08{\color{blue}{u_{n}}} -4050.
Or vn=un−3750v_n=u_n-3750 donc vn+3750=un{\color{blue}{v_{n} +3750=u_{n}}} . Ainsi :
vn+1=1,08×(vn+3750)−4050v_{n+1} =1,08\times{\color{blue}{\left(v_{n} +3750\right)}}-4050
vn+1=1,08vn+1,08×3750−4050v_{n+1} =1,08v_{n} +1,08\times 3750-4050
vn+1=1,08vn+4050−4050v_{n+1} =1,08v_{n} +4050-4050
vn+1=1,08vnv_{n+1} =1,08v_{n}

Question 4

En déduire la nature de la suite (vn)\left(v_n\right).

Correction
La suite (vn)\left(v_{n} \right) est géométrique de raison q=1,08q=1,08 et de premier terme v0=6250v_0=6250 . Le premier terme a été calculé à la question 22.
Question 5

Pour tout entier naturel nn, exprimer, vnv_n en fonction de nn.

Correction
  • L'expression de vnv_{n} en fonction de nn est donnée par la formule
    vn=v0×qnv_{n} =v_{0} \times q^{n}
Ainsi :
vn=6250×1,08nv_{n} =6250\times 1,08^{n}
Question 6

En déduire que pour tout entier naturel nn, on a un=6250×1,08n+3750u_n=6250 \times 1,08^n+3750.

Correction
On sait que vn=un−3750v_n=u_n-3750 donc vn+3750=unv_{n} +3750=u_{n}
Il vient alors que :
un=6250×1,08n+3750u_{n} =6250\times 1,08^{n}+3750

Question 7

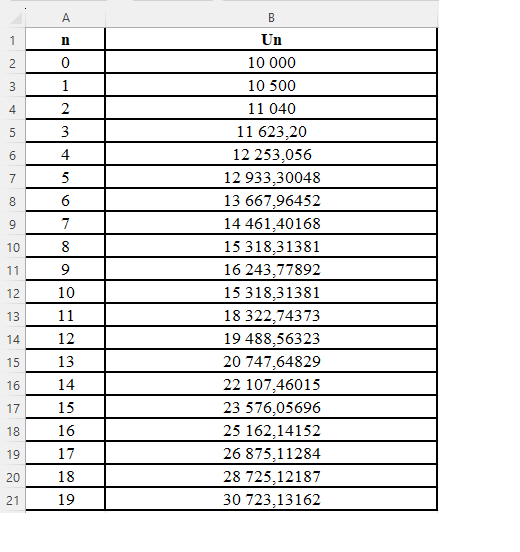Le tableau ci-dessus, extrait d'une feuille automatisée de calcul, a été obtenue par recopie vers le bas après avoir saisie la formule suivante dans la cellule B2 :
=6250∗1,08∧A2+3750=6250^* 1,08^{\wedge} \mathrm{A} 2+3750

La municipalité envisage d'ouvrir une nouvelle école maternelle dès que la population atteindra 1919 000000 habitants.
La construction d'un tel établissement nécessitant deux ans, déterminer l'année à partir de laquelle la construction de l'école doit commencer.

Correction
D'après la feuille de calcul, on peut lire que :
u11≈18322<19000u12≈19489>19000\begin{aligned}u_{11} & \approx18322<19000 \\u_{12} & \approx 19489>19000\end{aligned}
Comme unu_n représente le nombre d'habitants pour l'année 2020+n2020+n .
Cette nouvelle école ouvrira dans cette situation en 2020+12=20322020+12=2032 et il faudra commencer les travaux en 20302030.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.