Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Fonction exponentielle

Variations avec des fonctions de la forme x↦eax+bx\mapsto e^{ax+b} - Exercice 3

10 min
15
Question 1
Soit gg la fonction définie sur R\mathbb{R} par : g(t)=e−20tg\left(t\right)=e^{-20t}

Déterminer la fonction dérivée g′g' de gg .

Correction
  • (eax+b)′=aeax+b\left(e^{{\color{blue}a}x+{\color{red}b}} \right)^{'} ={\color{blue}a}e^{{\color{blue}a}x+{\color{red}b}}
    • gg est dérivable sur R\mathbb{R}.
    g(t)=e−20tg\left(t\right)=e^{{\color{blue}-20}t}
    Ici nous avons a=−20{\color{blue}a=-20} et b=0{\color{red}b=0} .
    Ainsi :
    g′(t)=−20×e−20tg'\left(t\right)={\color{blue}-20}\times e^{{\color{blue}-20}t}
    D'où
    g′(t)=−20e−20tg'\left(t\right)=-20e^{-20t}
    Question 2

    Etudier le signe de g′(t)g'\left(t\right) .

    Correction
    Nous savons que g′(t)=−20e−20tg'\left(t\right)=-20e^{-20t}
    Pour tout réel t∈Rt\in \mathbb{R} , on sait que e−20t>0e^{-20t}>0 . De plus −20<0-20<0 . Il en résulte donc que pour tout réel tt, on a : g′(t)<0g'\left(t\right)<0 .
    Question 3

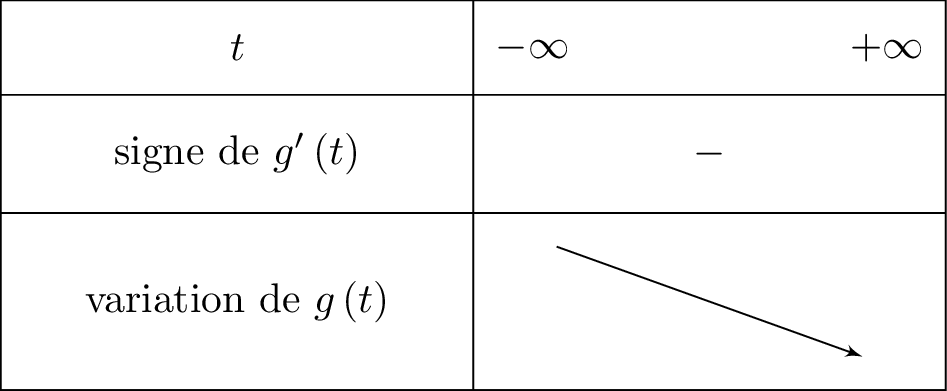
    En déduire les variations de gg sur R\mathbb{R} .

    Correction
    • Si f′f' est négative sur [a;b]\left[a;b\right] alors ff est décroissante sur [a;b]\left[a;b\right].
    • Si f′f' est positive sur [a;b]\left[a;b\right] alors ff est croissante sur [a;b]\left[a;b\right].
    Nous allons dresser le tableau de variation de ff.