Fonction exponentielle

Variations avec des fonctions de la forme eax+be^{ax+b} - Exercice 2

10 min
15
Question 1
Soit ff la fonction définie sur R\mathbb{R} par : f(x)=2e−4xf\left(x\right)=2e^{-4x}

Déterminer la fonction dérivée f′f' de ff .

Correction
  • (eax+b)′=aeax+b\left(e^{{\color{blue}a}x+{\color{red}b}} \right)^{'} ={\color{blue}a}e^{{\color{blue}a}x+{\color{red}b}}
    • ff est dérivable sur R\mathbb{R}.
    f(x)=2e−4xf\left(x\right)=2e^{{\color{blue}-4}x}
    Ici nous avons a=−4{\color{blue}a=-4} et b=0{\color{red}b=0} .
    Ainsi :
    f′(x)=2×(−4)×e−4xf'\left(x\right)=2\times\left({\color{blue}-4}\right)\times e^{{\color{blue}-4}x}
    D'où
    f′(x)=−8e−4xf'\left(x\right)=-8e^{-4x}
    Question 2

    Etudier le signe de f′(x)f'\left(x\right) .

    Correction
    Nous savons que f′(x)=−8e−4xf'\left(x\right)=-8e^{-4x}
    Pour tout réel x∈Rx\in \mathbb{R} , on sait que e−4x>0e^{-4x}>0 . De plus −8<0-8<0 . Il en résulte donc que pour tout réel xx, on a : f′(x)<0f'\left(x\right)<0 .
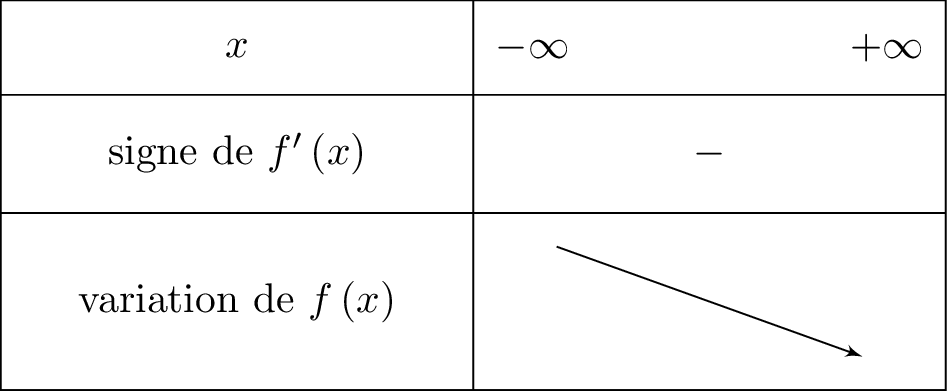
    Question 3

    En déduire les variations de ff sur R\mathbb{R} .

    Correction
    • Si f′f' est négative sur [a;b]\left[a;b\right] alors ff est décroissante sur [a;b]\left[a;b\right].
    • Si f′f' est positive sur [a;b]\left[a;b\right] alors ff est croissante sur [a;b]\left[a;b\right].
    Nous allons dresser le tableau de variation de ff.