Exercices types : Anciennement ÉPREUVES COMMUNES DE CONTRÔLE CONTINU $$1$$^ère partie - Exercice 3

$$f$$ est dérivable sur $$\left[0;10\right]$$ .
Ici on reconnaît la forme $$\left(uv\right)'=u'v+uv'$$ avec $$u\left(x\right)=3x$$ et $$v\left(x\right)=e^{{\color{blue}-0,4}x}$$.
Ainsi $$u'\left(x\right)=3$$ et $$v'\left(x\right)={\color{blue}-0,4}e^{{\color{blue}-0,4}x}$$.
Il vient alors que :
$$f'\left(x\right)=3e^{-0,4x} +3x\times \left(-0,4e^{-0,4x} \right)$$
$$f'\left(x\right)=3{\color{red}{e^{-0,4x}}} -1,2x{\color{red}{e^{-0,4x}}}$$ . Nous allons factoriser par $${\color{red}{e^{-0,4x}}}$$ . Il vient alors que :
$$f'\left(x\right)=e^{-0,4x} \left(3-1,2x\right)$$
Pour tout réel $$x$$, on a $$e^{-0,4x} >0$$.
$$3-1,2x\ge 0\Leftrightarrow -1,2x\ge -3\Leftrightarrow x\le \frac{-3}{-1,2} \Leftrightarrow x\le \frac{5}{2}$$
Cela signifie que l'on va mettre le signe $$+$$ dans la ligne de $$3-1,2x$$ lorsque $$x$$ sera inférieur ou égale à $$\frac{5}{2}$$.
Il en résulte donc que :

• si $$x\in\left[0;\frac{5}{2}\right]$$ alors $$f'\left(x\right)\ge0$$ et donc $$f$$ est croissante sur cet intervalle.
• si $$x\in\left[\frac{5}{2};10\right]$$ alors $$f'\left(x\right)\le0$$ et donc $$f$$ est décroissante sur cet intervalle.

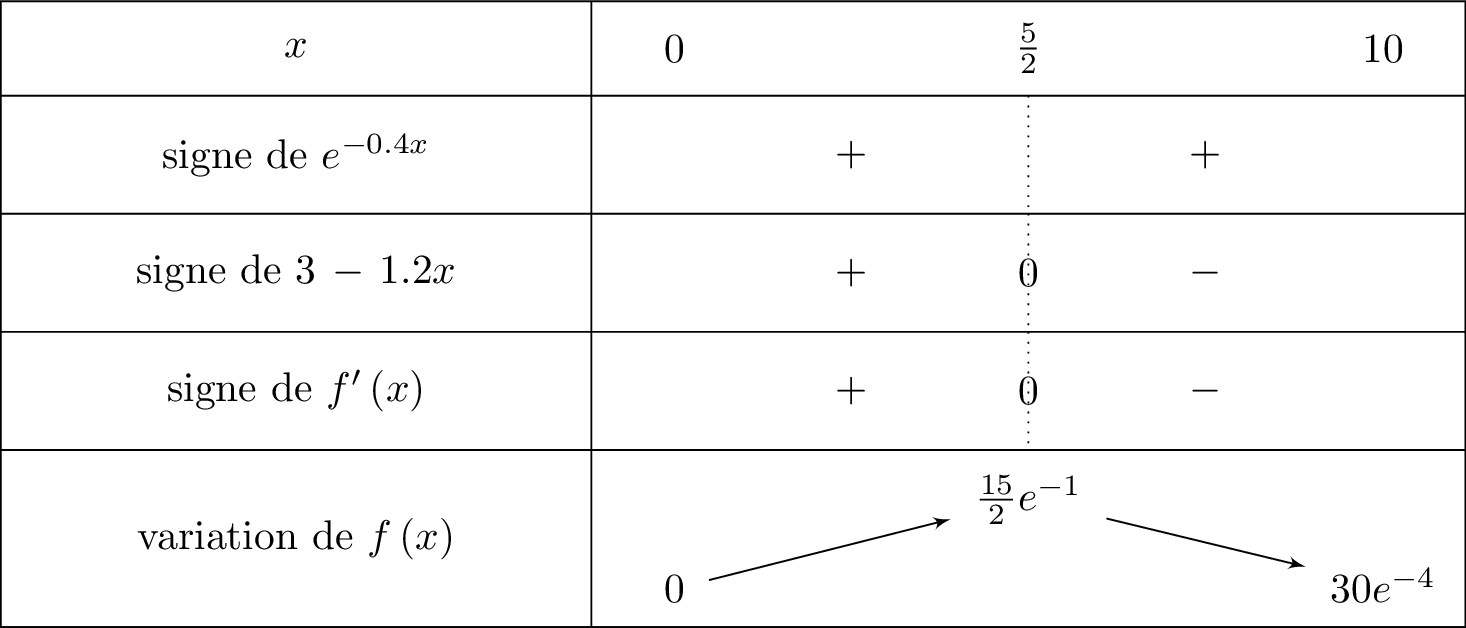
Nous traduisons toutes ces informations dans le tableau de variation ci-dessous :

$$f\left(0\right)=3\times 0\times e^{-0,4\times 0}\Leftrightarrow f\left(0\right)=0$$

$$f\left(\frac{5}{2}\right)=3\times \frac{5}{2}\times e^{-0,4\times \frac{5}{2}}\Leftrightarrow f\left(\frac{5}{2}\right)=\frac{15}{2}e^{-1}$$

$$f\left(10\right)=3\times 10\times e^{-0,4\times 10}\Leftrightarrow f\left(10\right)=30e^{-4}$$