Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : Anciennement ÉPREUVES COMMUNES DE CONTRÔLE CONTINU ère partie - Exercice 2
20 min
40
Une entreprise de menuiserie réalise des découpes dans des plaques rectangulaires de bois.
Dans un repère orthonormé d’unité cm ci-dessous, on modélise la forme de la découpe dans la plaque rectangulaire par la courbe représentative de la fonction définie sur l’intervalle par .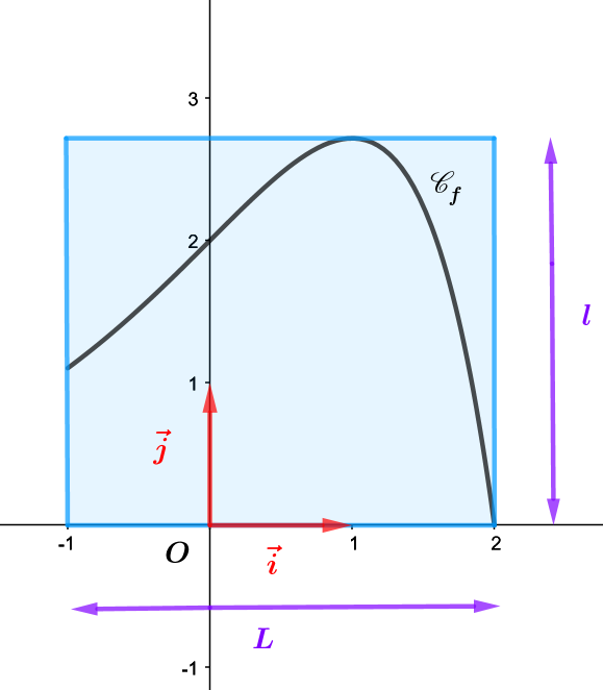
Dans un repère orthonormé d’unité cm ci-dessous, on modélise la forme de la découpe dans la plaque rectangulaire par la courbe représentative de la fonction définie sur l’intervalle par .

Question 1
Le bord supérieur de la plaque rectangulaire est tangent à la courbe . On nomme la longueur de la plaque rectangulaire et sa largeur.
On note la fonction dérivée de .
Montrer que pour tout réel de l'intervalle , on a : .
Montrer que pour tout réel de l'intervalle , on a : .
Correction
Soit .
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
. Il ne nous reste qu'à factoriser par .
Ainsi :
est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
. Il ne nous reste qu'à factoriser par .
Ainsi :
Question 2
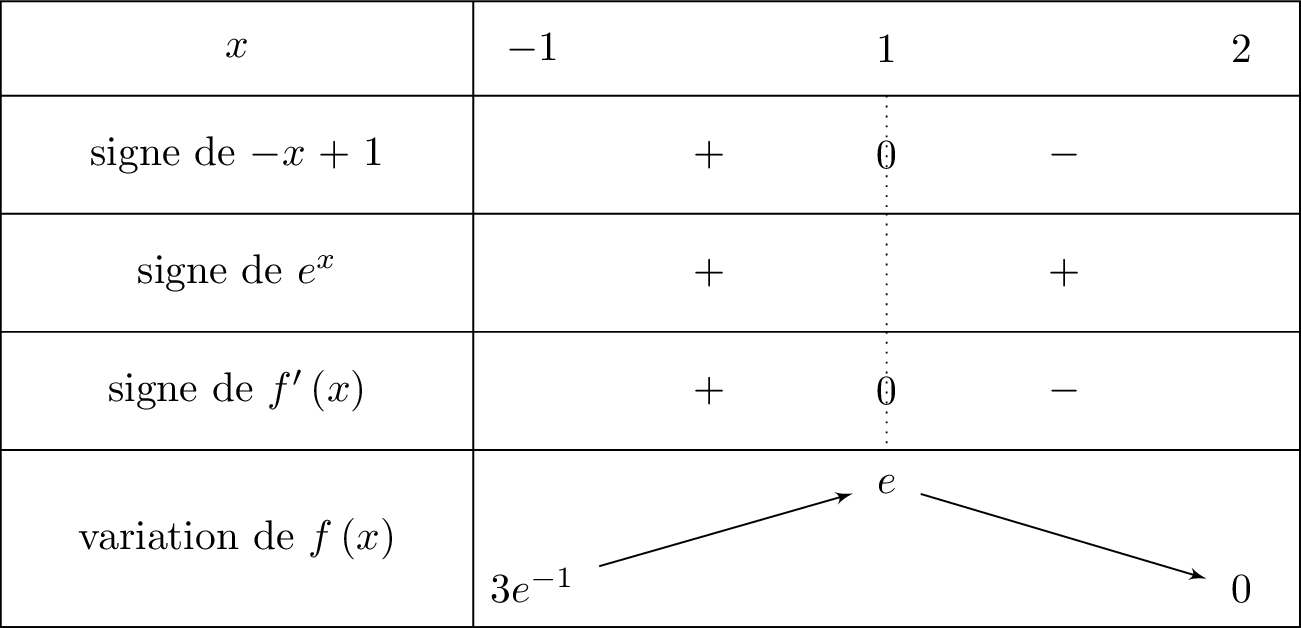
En déduire le tableau de variations de la fonction sur l'intervalle .
Correction
Nous savons que :
Pour tout réel , on a .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
Il en résulte donc que :
 De plus :
De plus :
d'où : d'où : d'où :
Pour tout réel , on a .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.

Question 3
La longueur de la plaque rectangulaire est de cm. Trouver sa largeur exacte en cm.
Correction
D'après les hypothèses de l'énoncé nous savons que le bord supérieur de la plaque rectangulaire est tangent à la courbe . On nomme la longueur de la plaque rectangulaire et sa largeur.
 Autrement dit, la valeur est atteinte lorsque qui correspond à l'abscisse du maximum de la fonction .
Autrement dit, la valeur est atteinte lorsque qui correspond à l'abscisse du maximum de la fonction .
Or nous savons que :
N'oublions pas que notre repère est orthonormé d’unité cm .
Il en résulte donc que : que l'on écrit

Or nous savons que :
N'oublions pas que notre repère est orthonormé d’unité cm .
Il en résulte donc que : que l'on écrit
cm
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.