Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
20 min
40
Un rameur est une machine d’exercice physique simulant les mouvements d’une personne qui fait de l’aviron.
Il est souvent utilisé pour l’entraînement sportif afin d’améliorer sa condition physique. La courbe ci-dessous représente la puissance (en Watt) en fonction du temps (en dixième de seconde) développée par un rameur débutant.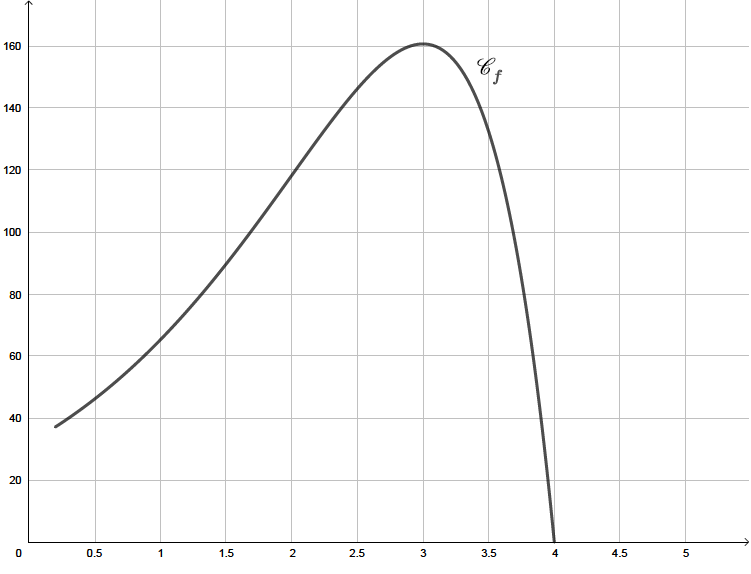
Il est souvent utilisé pour l’entraînement sportif afin d’améliorer sa condition physique. La courbe ci-dessous représente la puissance (en Watt) en fonction du temps (en dixième de seconde) développée par un rameur débutant.

Question 1
Répondre par lecture graphique aux deux questions suivantes.
Quelle est la puissance maximale atteinte par ce rameur ?
Correction
A l'aide du graphique ci-dessous, on peut en déduire la puissance maximale atteinte par ce rameur est de 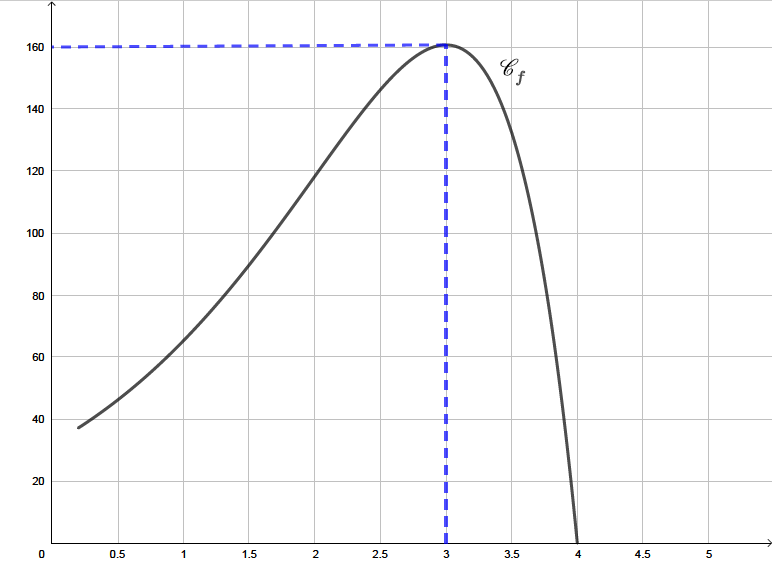

Question 2
Pendant combien de temps la puissance développée reste-t-elle au-dessus de Watts ?
Correction
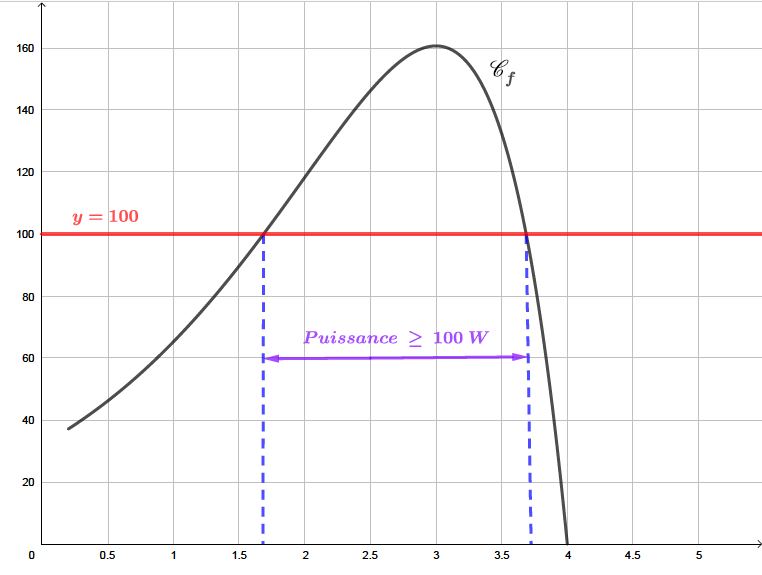
Question 3
Modélisation par une fonction
On suppose que la courbe est la courbe représentative de la fonction définie sur l’intervalle par :
On note la fonction dérivée de . On admet que pour tout réel de l’intervalle ,
On suppose que la courbe est la courbe représentative de la fonction définie sur l’intervalle par :
On note la fonction dérivée de . On admet que pour tout réel de l’intervalle ,
Étudier le signe de puis en déduire les variations de sur
Correction
Pour tout réel , on a . Le signe de dépend alors du signe de .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.
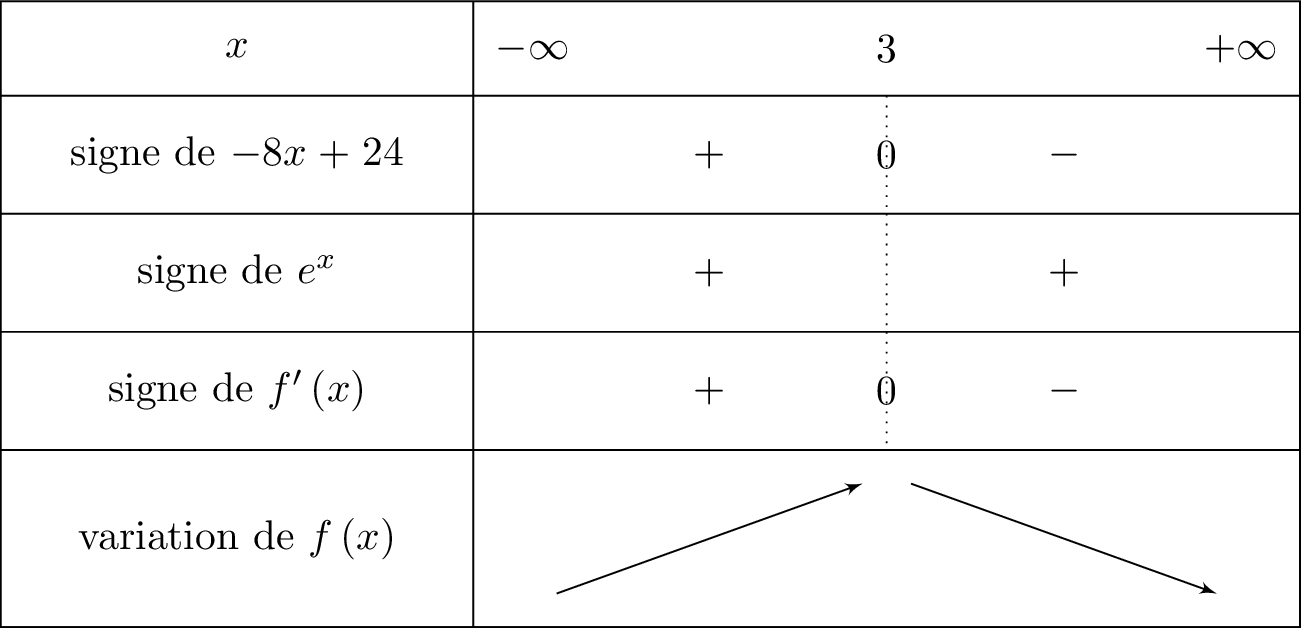
Question 4
Déterminer la valeur exacte du maximum de la fonction
Correction
D'après la question précédente, la fonction admet un maximum lorsque .
Ainsi : d'où :
La fonction admet un maximum dont la valeur exacte est lorsque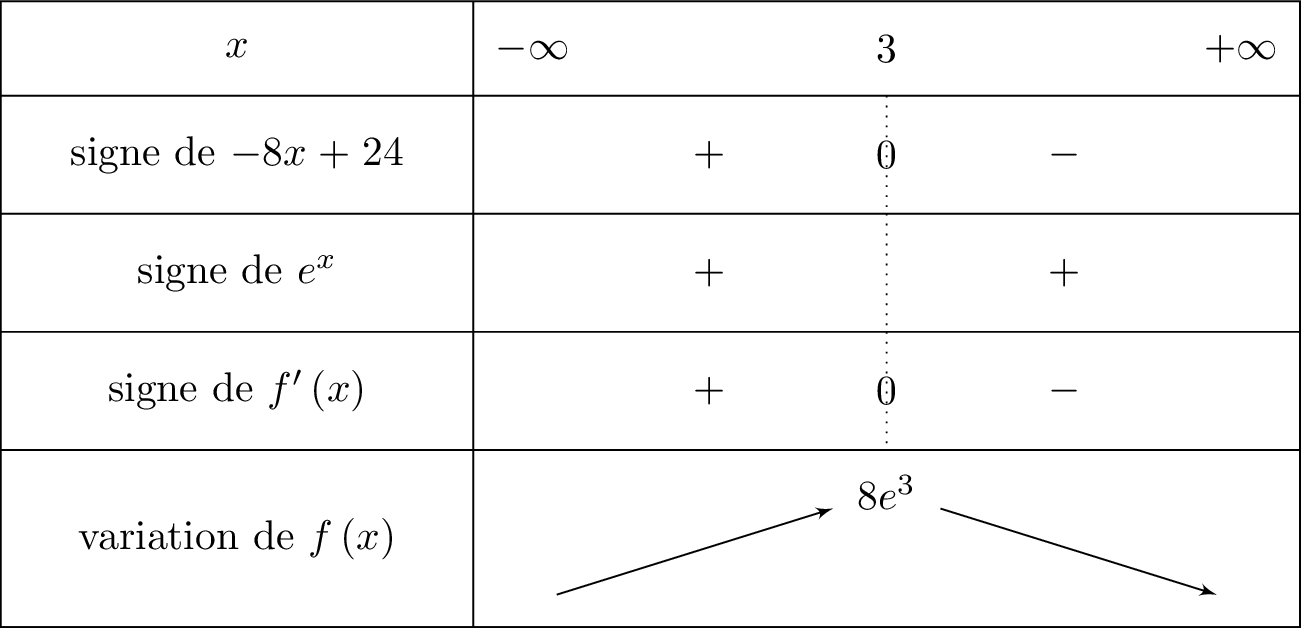
Ainsi : d'où :
La fonction admet un maximum dont la valeur exacte est lorsque

Question 5
On suppose que le sportif de tous les mois. Combien de mois d’entrainement seront-ils nécessaires pour qu’il dépasse les
Correction
On va modéliser la situation avec l'introduction d'une suite géométrique.
On introduit la suite dont le terme général est la performance maximale du sportif au bout de mois.
Chaque mois le sportif améliore sa meilleure performance de , il nous faut donc multiplier par le coefficient multiplicateur
Chaque terme se déduit du précédent en le multipliant par .
Il en résulte donc que la suite est de raison et de premier terme . En effet, on prend qui est la valeur maximale obtenue actuelle.
Ainsi, pour tout entier naturel , on a : .
Il en résulte donc que :
Maintenant, à l’aide de la calculatrice, nous obtenons les résultats suivants :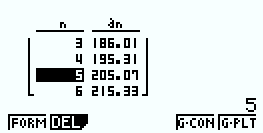 Nous pouvons donc lire avec une approximation à près que :
Nous pouvons donc lire avec une approximation à près que :
donc donc Finalement, c'est après mois le que sportif dépassera les Watts .
On introduit la suite dont le terme général est la performance maximale du sportif au bout de mois.
Chaque mois le sportif améliore sa meilleure performance de , il nous faut donc multiplier par le coefficient multiplicateur
Chaque terme se déduit du précédent en le multipliant par .
Il en résulte donc que la suite est de raison et de premier terme . En effet, on prend qui est la valeur maximale obtenue actuelle.
Ainsi, pour tout entier naturel , on a :
Soit une suite géométrique. L'expression de en fonction de est :
: lorsque le premier terme vaut .
Dans notre cas, le premier terme ici vaut .Il en résulte donc que :
Maintenant, à l’aide de la calculatrice, nous obtenons les résultats suivants :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.