Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
15 min
30
Soit la ligne brisée représentée ci-dessous, où et sont colinéaires et de même sens.
La figure complète l'énoncé ci-dessus.
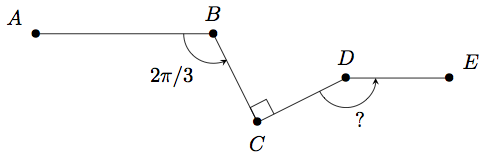
La figure complète l'énoncé ci-dessus.

Question 1
Traduire les données de l'énoncé (figure + texte) en termes d'angles orientés de vecteurs.
Correction
Soient deux vecteurs et .
D'après l'énoncé, les vecteurs et sont colinéaires et de même sens. - Si les vecteurs et sont colinéaires et de même sens alors l'angle orienté
- Si les vecteurs et sont colinéaires et de sens opposés alors l'angle orienté
Cela signifie que : .
De plus, à l'aide de la représentation de la ligne brisée, on lit facilement que :
Question 2
Déterminer une mesure de l'angle orienté
Correction
D'après la relation de Chasles, on a :
Comme : ; et , il vient alors que :
Nous allons déterminer la mesure principale de .
« A la calculatrice, on tape . On s'intéresse uniquement à la partie entière c'est à dire à la partie avant la virgule. Ici on a . Comme est impair on rajoute ce qui nous donne . On garde cette valeur. On va soustraire à la valeur qui est bien un multiple de »
La partie entre guillemets et en italique est une explication pour obtenir la mesure principale.
Vous ne devez pas l'écrire sur une copie.
Ce qui doit apparaitre sur une copie est donnée ci-dessous :
Il vient alors :
Il en résulte que la mesure principale de l'angle orienté de mesure est .
Ainsi :
Comme : ; et , il vient alors que :
Nous allons déterminer la mesure principale de .
« A la calculatrice, on tape . On s'intéresse uniquement à la partie entière c'est à dire à la partie avant la virgule. Ici on a . Comme est impair on rajoute ce qui nous donne . On garde cette valeur. On va soustraire à la valeur qui est bien un multiple de »
La partie entre guillemets et en italique est une explication pour obtenir la mesure principale.
Vous ne devez pas l'écrire sur une copie.
Ce qui doit apparaitre sur une copie est donnée ci-dessous :
Il vient alors :
Il en résulte que la mesure principale de l'angle orienté de mesure est .
Ainsi :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.