Probabilités conditionnelles : ce qu'il faut savoir pour le contrôle - Exercice 1

10 min
25
On considère deux évènements AA et BB d'un même univers.
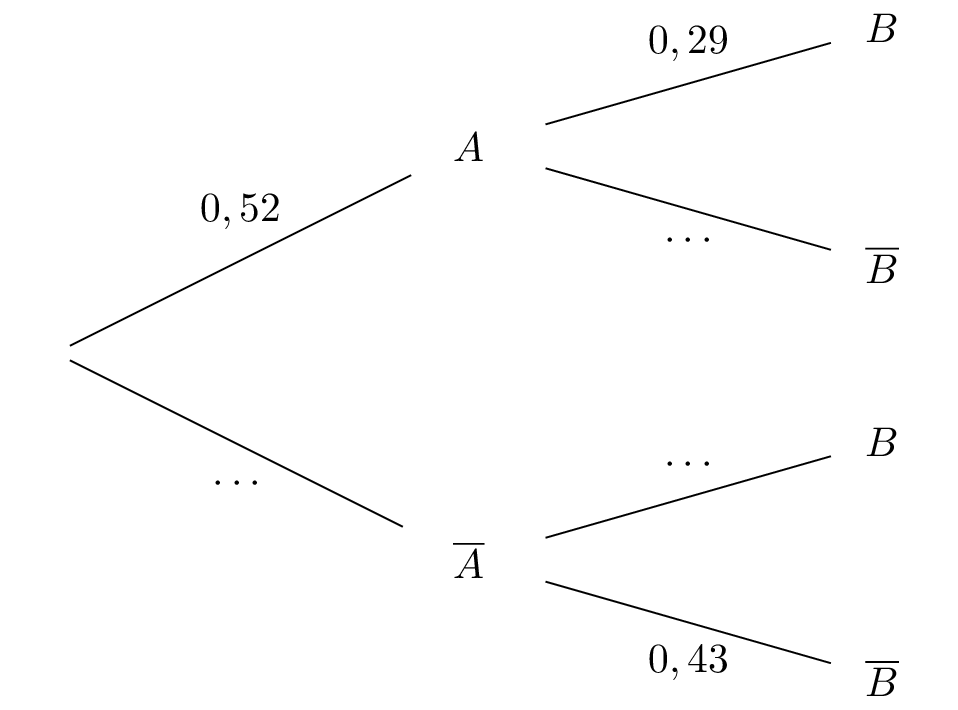
Soit l'arbre de probabilité ci-dessous :
Question 1

Indiquer ce que signifie les valeurs 0,520,52 ; 0,290,29 et 0,430,43 .

Correction
Nous donnons ci-dessous l'arbre pondéré remplit de manière théorique, comme vu en cours. Sur chaque branche, apparaisse les noms des probabilités correspondantes.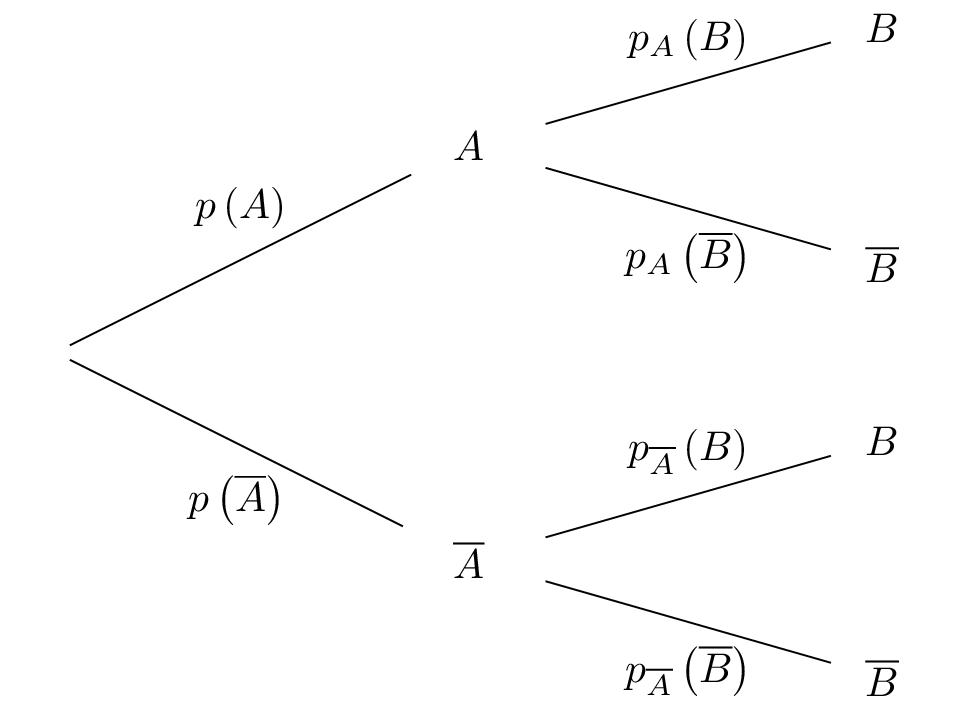
Il en résulte donc que :
  • p(A)=0,52p\left(A\right)=0,52
  • pA‾(B‾)=0,43p_{\overline{A}}\left(\overline{B}\right)=0,43
  • pA(B)=0,29p_A\left(B\right)=0,29
    • Question 2

    Compléter l'arbre de probabilité donnée ci-dessus.

    Correction
    D'après les hypothèses, nous savons que :
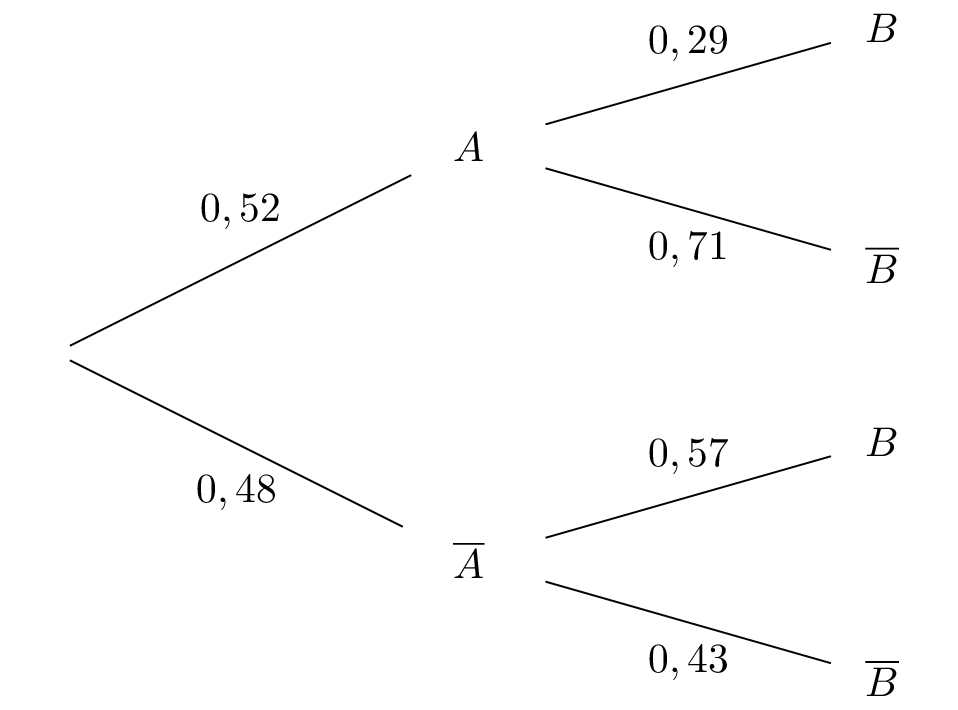
    • La somme des probabilités issues d'un même nœud est égale à 11.
    Ainsi :
  • p(A‾)=1−p(A)=1−0,52=0,48p\left(\overline{A}\right)=1-p\left(A\right)=1-0,52=0,48
  • pA(B‾)=1−pA(B)=1−0,29=0,71p_{A}\left(\overline{B}\right)=1- p_{A}\left(B\right)=1-0,29=0,71
  • pA‾(B)=1−pA‾(B‾)=1−0,43=0,57p_{\overline{A}}\left(B\right)=1- p_{\overline{A}}\left(\overline{B}\right)=1-0,43=0,57
    • Ce qui nous donne :
    Question 3

    Calculer la probabilité p(A∩B)p\left(A\cap B\right) .

    Correction
    Pour calculer la probabilité p(A∩B)p\left(A\cap B\right) il nous suffit de faire le produit des probabilités des branches passant par le chemin AA puis par BB.
    Ainsi :
    p(A∩B)=p(A)×pA(B)p\left(A\cap B\right)=p\left(A\right)\times p_A\left(B\right)
    p(A∩B)=0,52×0,29p\left(A\cap B\right)=0,52\times0,29
    D'où :
    p(A∩B)=0,1508p\left(A\cap B\right)=0,1508
    Question 4

    Calculer la probabilité p(A‾∩B)p\left(\overline{A}\cap B\right) .

    Correction
    Pour calculer la probabilité p(A‾∩B)p\left(\overline{A}\cap B\right) il nous suffit de faire le produit des probabilités des branches passant par le chemin A‾\overline{A} puis par BB.
    Ainsi :
    p(A‾∩B)=p(A‾)×pA‾(B)p\left(\overline{A}\cap B\right)=p\left(\overline{A}\right)\times p_{\overline{A}}\left(B\right)
    p(A‾∩B)=0,48×0,57p\left(\overline{A}\cap B\right)=0,48\times0,57
    D'où :
    p(A‾∩B)=0,2736p\left(\overline{A}\cap B\right)=0,2736
    Question 5

    En déduire la probabilité de p(B)p\left(B\right) .

    Correction
    p(B)p\left(B\right) est la probabilité des chemins qui arrivent en BB .
    Cela se traduit par :
    p(B)=p(A∩B)+p(A‾∩B)p\left(B\right)=p\left(A\cap B\right)+p\left(\overline{A}\cap B\right)
    p(B)=0,1508+0,2736p\left(B\right)=0,1508+0,2736
    Ainsi :
    p(B)=0,4244p\left(B\right)=0,4244

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.