Fonction logarithme népérien
Exercice 5 - Exercice 1
1 min
0
Des Suites avec des Logarithmes :)
Question 1
On appelle la fonction définie sur l'intervalle par . On note la courbe représentative de la fonction .
On considère également une fonction définie sur l'intervalle par .
On considère également une fonction définie sur l'intervalle par .
Calculer la limite de la fonction en .
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer . Le tableau de signe ci-dessous nous explique pourquoi
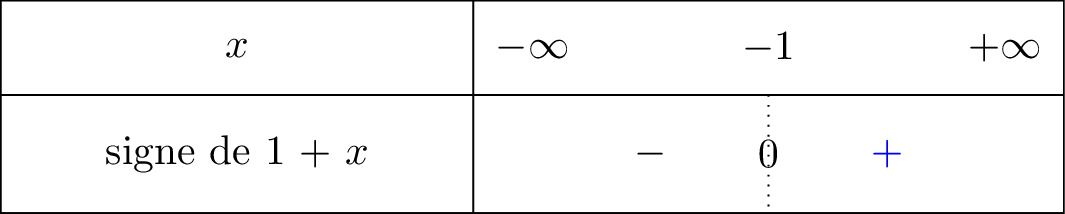 On pose .
On pose .
Ainsi : .
Par composition :
Ainsi :
On commence par calculer . Le tableau de signe ci-dessous nous explique pourquoi

Ainsi : .
Par composition :
Ainsi :
Question 2
Calculer la limite de la fonction en .
Correction
Question 3
On note la fonction dérivée de . Calculer pour tout de l’intervalle .
Correction
Soit .
est dérivable sur .
est dérivable sur .
Question 4
Etudier les variations de la fonction sur l'intervalle .
Correction
Il nous faut étidier le signe de :
Comme alors et donc . Le dénominateur est donc strictement positif.
De plus, nous savons que ainsi . De ce fait , , ce qui signifie que le numérateur est positif.
Il en résulte donc que :
. Ce qui signifie que la fonction est strictement croissante sur .
Nous dressons ci-dessous, le tableau de variation de la fonction en y intégrant les limites déterminées précédemment.
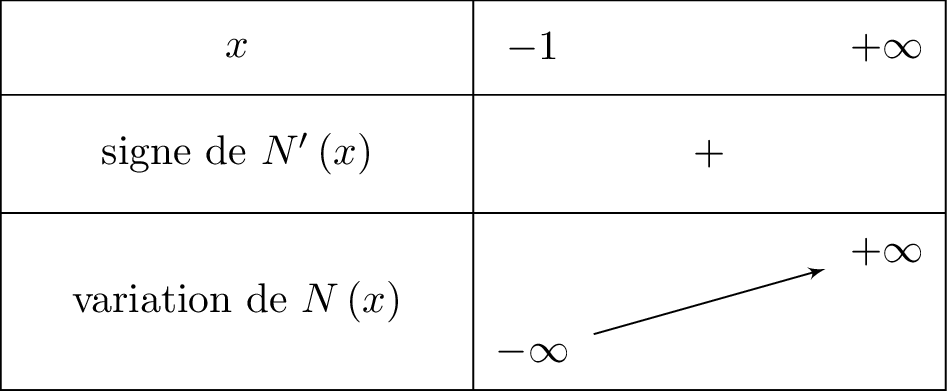
Comme alors et donc . Le dénominateur est donc strictement positif.
De plus, nous savons que ainsi . De ce fait , , ce qui signifie que le numérateur est positif.
Il en résulte donc que :
. Ce qui signifie que la fonction est strictement croissante sur .
Nous dressons ci-dessous, le tableau de variation de la fonction en y intégrant les limites déterminées précédemment.

Question 5
Calculer et en déduire le signe de sur l'intervalle .
Correction
Soit ainsi :
d'où
Il vient que :
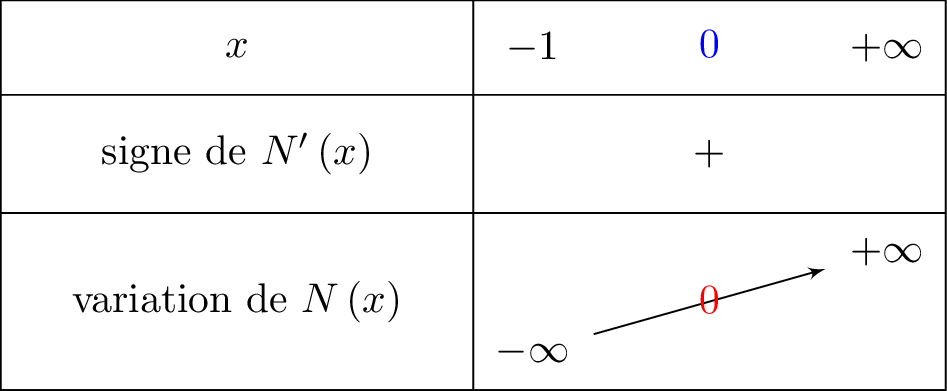
Sur , la fonction est continue et strictement croissante.
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que et nous savons que .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :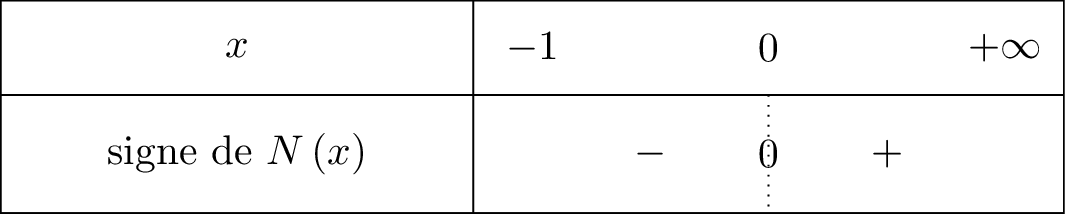
d'où
Il vient que :
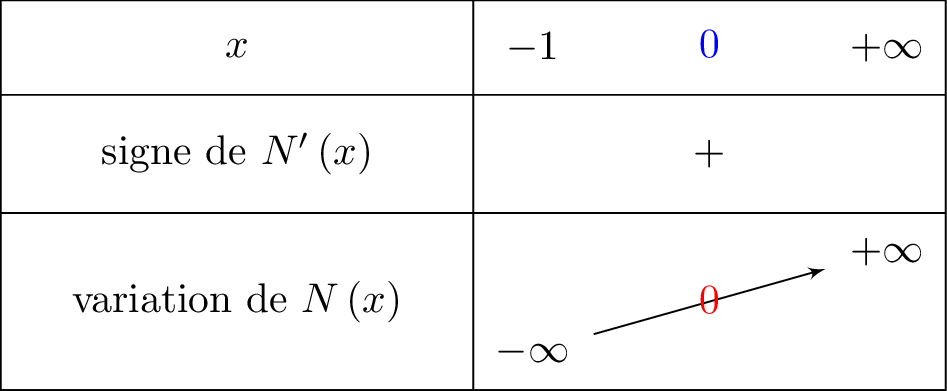
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que et nous savons que .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 6
On note la fonction dérivée de . Calculer pour tout de l’intervalle et montrer que
Correction
Soit
est dérivable sur .
On reconnaît la forme avec ; et .
Ainsi ; et .
est dérivable sur .
On reconnaît la forme avec ; et .
Ainsi ; et .
Question 7
En déduire les variations de la fonction . On ne demandera pas les limites.
Correction
D'après la question , nous savons que :
Or pour tout , nous vérifions facilement que ( vu aussi à la question )
Donc le signe de dépend du signe de .
Or, d'après la question , nous avons déterminer le signe de . Nous pouvons donc dresser le tableau de variation de la fonction .
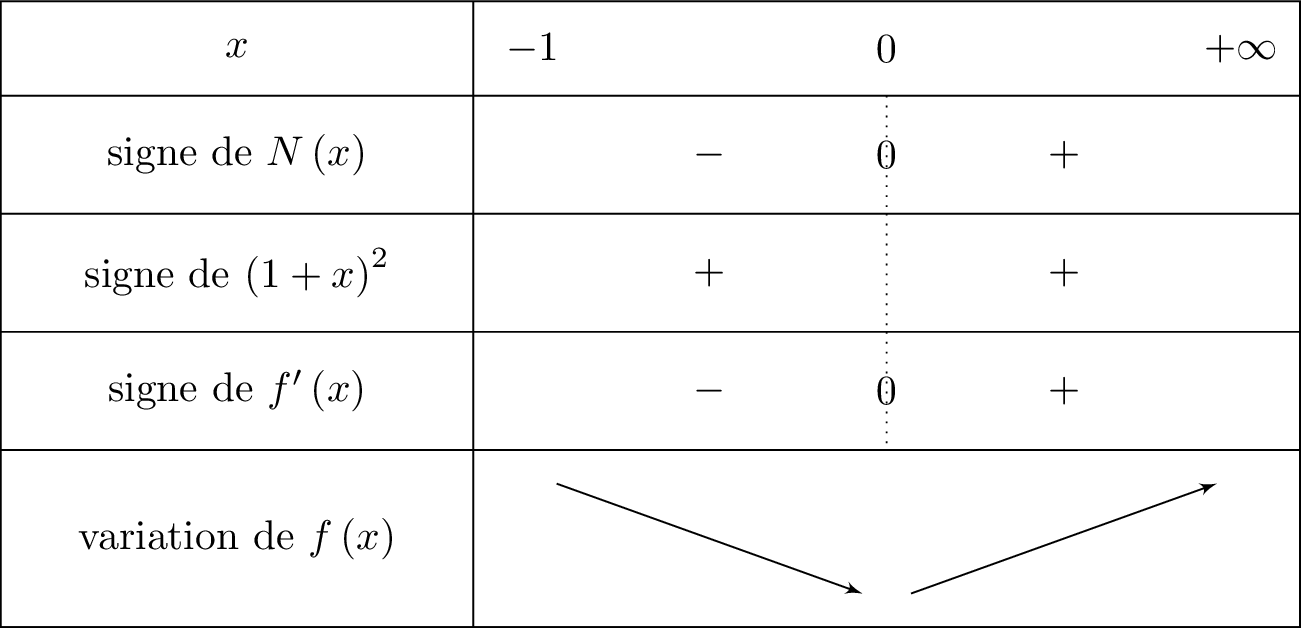
Or pour tout , nous vérifions facilement que ( vu aussi à la question )
Donc le signe de dépend du signe de .
Or, d'après la question , nous avons déterminer le signe de . Nous pouvons donc dresser le tableau de variation de la fonction .

Question 8
Démontrer que si , alors .
Correction
Nous savons que les variations de la fonction dont données par le tableau ci-dessous :
 Nous allons faire une rescription de la fonction sur l'intervalle .
Nous allons faire une rescription de la fonction sur l'intervalle .
d'où d'où et Il vient alors que : 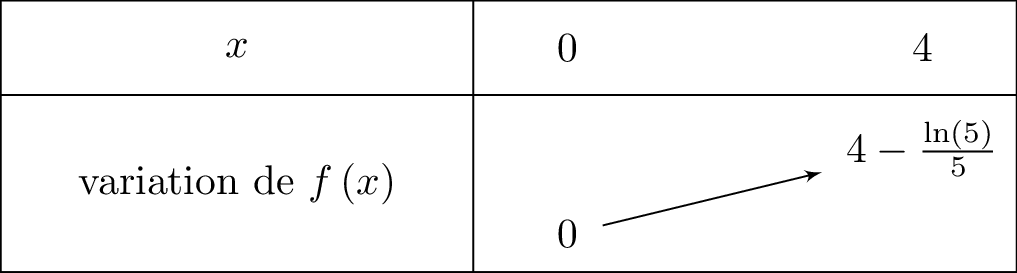 Comme alors :
Comme alors :
car la fonction est croissante sur donc l'ordre est conservé .
Ainsi si , alors .


car la fonction est croissante sur donc l'ordre est conservé .
Ainsi si , alors .