Fonction logarithme népérien

Exercice 4 - Exercice 1

1 min
0
On considère la fonction ff définie sur l’intervalle ]0;3]\left]0; 3\right] par f(x)=x2(1−ln⁡(x))f\left(x\right)=x^{2} \left(1-\ln \left(x\right)\right)
On donne ci-dessous sa courbe représentative C\mathscr{C}.
Question 1
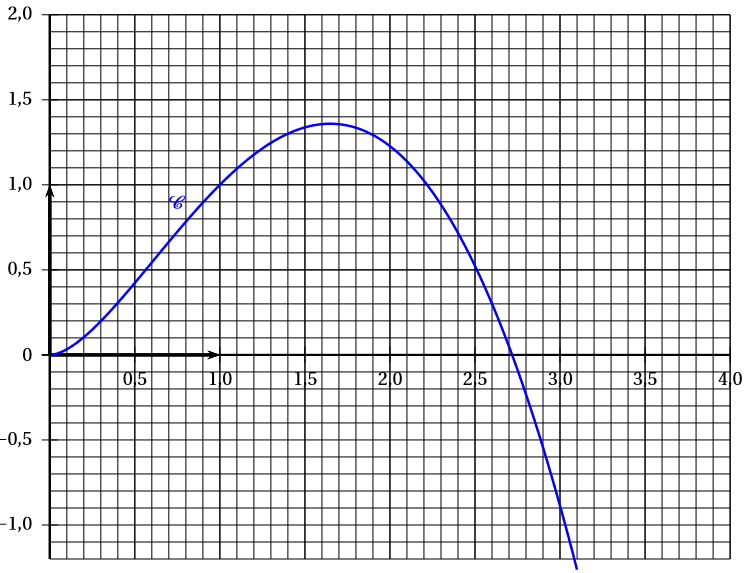
On admet que ff est deux fois dérivable sur ]0;3]\left]0; 3\right], on note f′f' sa fonction dérivée et on admet que sa dérivée seconde f′′f'' est définie sur ]0;3]\left]0; 3\right] par : f′′(x)=−1−2ln⁡(x)f''\left(x\right)=-1-2\ln \left(x\right)

Sur ]0;3]\left]0; 3\right], C\mathscr{C} coupe l’axe des abscisses au point d’abscisse :
  • ee
  • 00 et ee
  • 12e+1\frac{1}{2}e+1

Correction
La bonne réponse est aa.
C\mathscr{C} coupe l’axe des abscisses au point d’abscisse signifie qu'il nous faut résoudre l'équation f(x)=0f\left(x\right)=0.
f(x)=0f\left(x\right)=0 équivaut successivement à :
x2(1−ln⁡(x))=0x^{2} \left(1-\ln \left(x\right)\right)=0. Il s'agit d'une équation produit
x2=0x^{2} =0 ou 1−ln⁡(x)=01-\ln \left(x\right)=0
Résolvons d'une part :
x2=0⇔x=0x^{2} =0\Leftrightarrow x=0. Or il ne faut pas oublier que nous travaillons sur l'intervalle ]0;3]\left]0; 3\right]. Cela signifie que l'on ne retiendra pas la solution x=0x=0.
Résolvons d'autre part :
1−ln⁡(x)=0⇔−ln⁡(x)=−1⇔ln⁡(x)=1⇔ln⁡(x)=ln⁡(e)⇔x=e1-\ln \left(x\right)=0\Leftrightarrow -\ln \left(x\right)=-1\Leftrightarrow \ln \left(x\right)=1\Leftrightarrow \ln \left(x\right)=\ln \left(e\right)\Leftrightarrow x=e
Dans ce cas de figure, la valeur x=ex=e appartient bien à l'intervalle ]0;3]\left]0; 3\right].
Il en résulte donc que l'équation f(x)=0f\left(x\right)=0 admet donc une seule solution
x=ex=e
.
Question 2

f′′(x)=0f''\left(x\right)=0 lorsque :
  • ee
  • 1e\frac{1}{\sqrt{e} }
  • e\sqrt{e}

Correction
La bonne réponse est bb.
f′′(x)=0f''\left(x\right)=0 équivaut successivement à :
−1−2ln⁡(x)=0-1-2\ln \left(x\right)=0
−2ln⁡(x)=1-2\ln \left(x\right)=1
ln⁡(x)=−12\ln \left(x\right)=-\frac{1}{2}
  • ln⁡ea=a\ln e^{a }=a
ln⁡(x)=ln⁡e−12\ln \left(x\right)=\ln e^{-\frac{1}{2} }
x=e−12x=e^{-\frac{1}{2} }
  • e−a=1eae^{-a }=\frac{1}{e^{a}}
x=1e12x=\frac{1}{e^{\frac{1}{2} } }
  • e12=ee^{\frac{1}{2} }=\sqrt{e}
x=1ex=\frac{1}{\sqrt{e} }

Question 3

Pour tout nombre réel xx de l’intervalle ]0;3]\left]0; 3\right] on a :
  • f′(x)=x(1−2ln⁡(x))f'\left(x\right)=x\left(1-2\ln \left(x\right)\right)
  • f′(x)=−2xf'\left(x\right)=-\frac{2}{x}
  • f′(x)=−2f'\left(x\right)=-2

Correction
La bonne réponse est aa.
ff est dérivable sur ]0;3]\left]0; 3\right]
Ici on reconnaît la forme : (uv)′=u′v+uv′\left(uv\right)'=u'v+uv' avec u(x)=x2u\left(x\right)=x^{2} et v(x)=1−ln⁡(x)v\left(x\right)=1-\ln \left(x\right).
Ainsi : u′(x)=2xu'\left(x\right)=2x et v′(x)=−1xv'\left(x\right)=-\frac{1}{x} .
Il vient alors que :
f′(x)=2x(1−ln⁡(x))+x2×(−1x)f'\left(x\right)=2x\left(1-\ln \left(x\right)\right)+x^{2} \times \left(-\frac{1}{x} \right)
f′(x)=2x(1−ln⁡(x))−x2xf'\left(x\right)=2x\left(1-\ln \left(x\right)\right)-\frac{x^{2} }{x}
f′(x)=2x(1−ln⁡(x))−xf'\left(x\right)=2x\left(1-\ln \left(x\right)\right)-x
f′(x)=2x−2xln⁡(x)−xf'\left(x\right)=2x-2x\ln \left(x\right)-x
f′(x)=x−2xln⁡(x)f'\left(x\right)=x-2x\ln \left(x\right)
f′(x)=x(1−2ln⁡(x))f'\left(x\right)=x\left(1-2\ln \left(x\right)\right)

Question 4

Une équation de la tangente à C\mathscr{C} au point d’abscisse ee s’écrit :
  • y=−x+ey=-x+e
  • y=−exy=-ex
  • y=−ex+e2y=-ex+e^{2}

Correction
La bonne réponse est cc.
L'équation de la tangente au point d'abscisse aa s'écrit y=f′(a)(x−a)+f(a)y=f'\left(a\right)\left(x-a\right)+f\left(a\right).
Ici a=ea=e, ce qui donne, y=f′(e)(x−e)+f(e)y=f'\left(e\right)\left(x-e\right)+f\left(e\right).
1ère étape : calculer f(e)f\left(e\right)
f(e)=e2(1−ln⁡(e))f\left(e\right)=e^{2} \left(1-\ln \left(e\right)\right)
f(e)=e2(1−1)f\left(e\right)=e^{2} \left(1-1\right)
f(e)=e2×0f\left(e\right)=e^{2}\times0
f(e)=0f\left(e\right)=0
2ème étape : calculer f′(e)f'\left(e\right)
f′(e)=e(1−2ln⁡(e))f'\left(e\right)=e\left(1-2\ln \left(e\right)\right)
f′(e)=e(1−2)f'\left(e\right)=e\left(1-2\right)
f′(e)=e×(−1)f'\left(e\right)=e\times\left(-1\right)
f′(e)=−ef'\left(e\right)=-e
3ème étape : on remplace les valeurs de f(e)f\left(e\right) et de f′(e)f'\left(e\right) dans la formule de l'équation de tangente.
On sait que :
y=f′(e)(x−e)+f(e)y=f'\left(e\right)\left(x-e\right)+f\left(e\right)
y=−e×(x−e)+0y=-e\times \left(x-e\right)+0
y=−ex+e2y=-ex+e^{2}
Ainsi l'équation de la tangente à la courbe C\mathscr{C} au point d'abscisse ee est alors :
y=−ex+e2y=-ex+e^{2}
.