Fonction logarithme népérien
Exercice 3 - Exercice 1
1 min
0
Soit la fonction définie sur par : où et sont des constantes réelles.
On appelle la courbe représentative de la fonction dans un repère orthogonal .
Le point appartient à .
admet une tangente horizontale en son point d’abscisse .
On appelle la courbe représentative de la fonction dans un repère orthogonal .
Le point appartient à .
admet une tangente horizontale en son point d’abscisse .
Question 1
PARTIE A
Sur le graphique ci-dessous, on a tracé (trait plein) ainsi que les courbes et .
L’une de ces deux courbes est la représentation graphique de la fonction dérivée de et l’autre représente une primitive de .
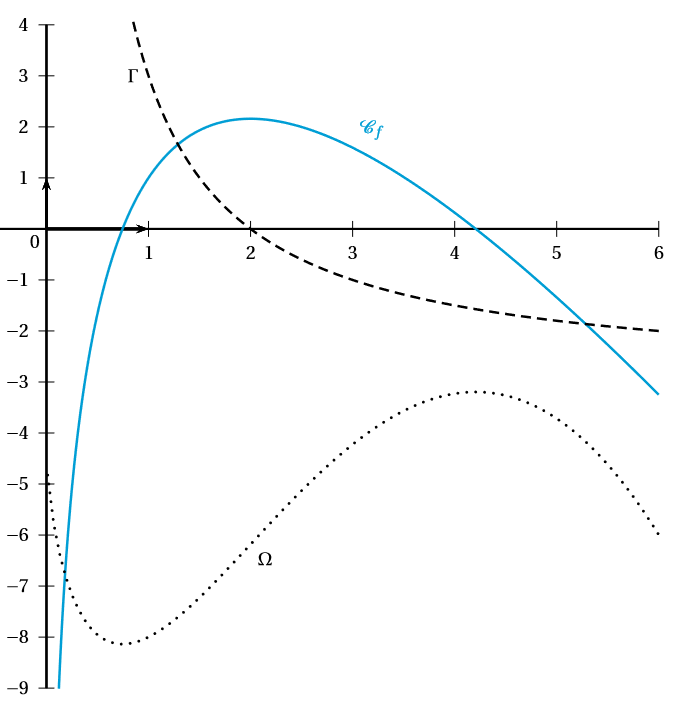
Sur le graphique ci-dessous, on a tracé (trait plein) ainsi que les courbes et .
L’une de ces deux courbes est la représentation graphique de la fonction dérivée de et l’autre représente une primitive de .

Indiquer laquelle des deux courbes est la représentation graphique de .
Correction
- Lorsque est positive sur alors est croissante sur
- Lorsque est négative sur alors est décroissante sur
Ainsi la représentation graphique de sa primitive devrait être donc commencer par être décroissante, croissante et enfin décroissante.
Or la représentation graphique de la courbe est uniquement décroissante. Elle ne peut donc pas correspondre à la représentation graphique de .
Finalement, La courbe est la représentation graphique de .
Question 2
Par lecture graphique, déterminer et .
Correction
Le point appartient à , il vient alors que
La courbe admet une tangente horizontale en son point d’abscisse . Or le coefficient directeur d'une tangente horizontale est nulle. Par définition, correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .
Ainsi
.
La courbe admet une tangente horizontale en son point d’abscisse . Or le coefficient directeur d'une tangente horizontale est nulle. Par définition, correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .
Ainsi
Question 3
Donner l’expression de en fonction de et de .
Correction
est dérivable sur .
On obtient alors :
On obtient alors :
Question 4
À l’aide des résultats précédents, montrer que pour tout de l’intervalle , on a :
Correction
D'après les questions précédentes, nous savons que : et .
D'une part : équivaut successivement à :
D'autre part : équivaut successivement à :
Finalement : .
Finalement : .
Question 5
PARTIE B
Dans cette partie, on pourra vérifier la cohérence des résultats obtenus avec la courbe fournie dans la partie .
Dans cette partie, on pourra vérifier la cohérence des résultats obtenus avec la courbe fournie dans la partie .
Calculer la limite de la fonction lorsque tend vers . Interpréter graphiquement cette limite.
Correction
- Si alors la fonction admet une asymptote verticale d'équation
- Si alors la fonction admet une asymptote verticale d'équation
Question 6
Calculer .
Correction
est dérivable sur .
On obtient alors :
. Nous allons mettre l'expression au même dénominateur.
On obtient alors :
. Nous allons mettre l'expression au même dénominateur.
Question 7
Etudier le signe de puis donner les variations de la fonction .
Correction
Pour tout réel , on vérifie que .
Le signe de dépend alors uniquement de son numérateur .
Il en résulte donc que :
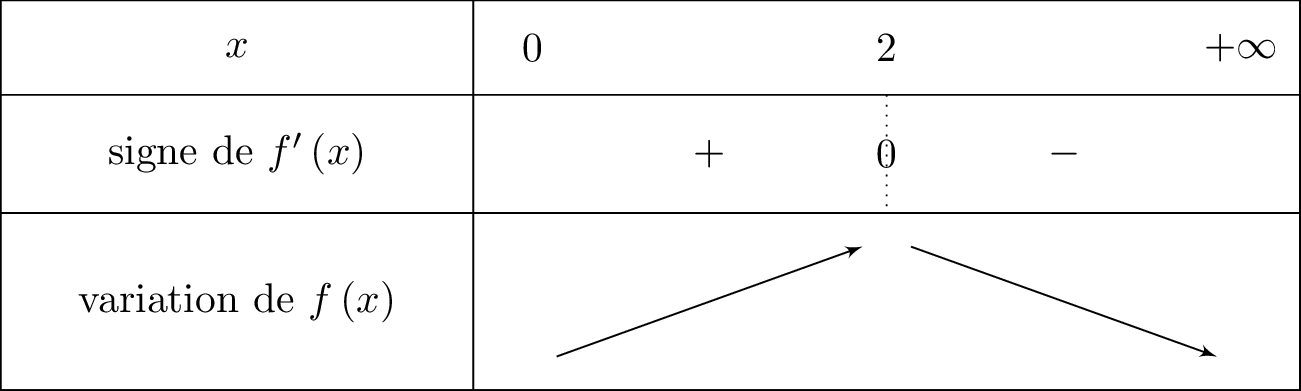
Le signe de dépend alors uniquement de son numérateur .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.

Question 8
En déduire que la fonction admet un extremum dont on calculera la valeur exacte.
Correction
La fonction admet un extremum, qui correspond à un maximum, lorsque .
Ainsi :
Nous donnons ci-dessous le tableau de variation complet de .
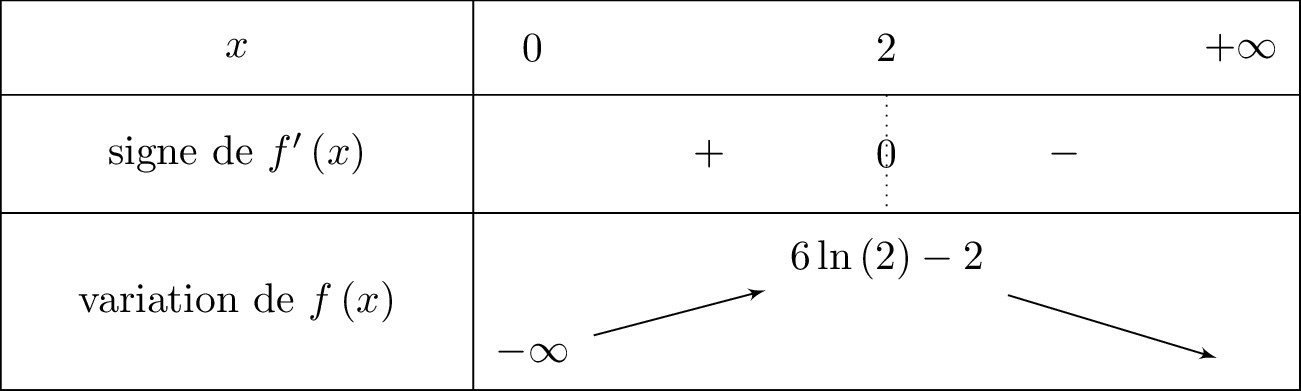
Ainsi :
Nous donnons ci-dessous le tableau de variation complet de .

Question 9
Soit la fonction définie sur par :
Montrer que est une primitive de sur .
Correction
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que
Soit : .Autrement dit, il faut que
On reconnaît la forme : avec ; et .
Ainsi : ; et .
Il vient alors que :
Ainsi :
On a bien montré que est une primitive de sur .
Question 10
Calculer la valeur exacte de .
Correction
équivaut successivement à :