Fonction logarithme népérien
Exercice 2 - Exercice 1
1 min
0
PARTIE A
est une fonction définie et dérivable sur l’intervalle .
désigne la fonction dérivée de .
est une fonction définie et dérivable sur l’intervalle .
désigne la fonction dérivée de .
Question 1
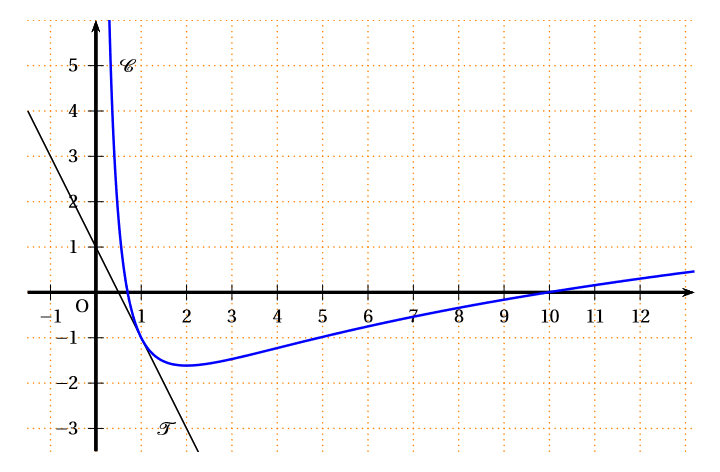
- est la représentation graphique de la fonction dans un repère orthonormal.
- est la tangente à au point de coordonnées .
- passe par le point de coordonnées .
Par lecture graphique, déterminer .
Correction
On lit à l'aide du graphique que
.
Question 2
Déterminer .
Correction
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .
Notons le point appartenant donc à la tangente . De plus , vec les hypothèses, nous savons que passe par le point de coordonnées . Nous allons donc appelé ce point
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Notons le point appartenant donc à la tangente . De plus , vec les hypothèses, nous savons que passe par le point de coordonnées . Nous allons donc appelé ce point
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Question 3
Donner une équation de .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .D'après les questions précédentes, nous savons que : et
On remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors :
.
Question 4
On sait que est de la forme où et sont des nombres réels.
Calculer .
Correction
est dérivable sur .
Il vient alors que :
équivaut successivement à :
équivaut successivement à :
Question 5
Déterminer alors les valeurs de et .
Correction
D'après les questions précédentes, nous savons que : et .
D'une part : équivaut successivement à :
D'autre part : équivaut successivement à :
Finalement : .
Finalement : .
Question 6
PARTIE B.
Soit la fonction définie et dérivable sur par .
Soit la fonction définie et dérivable sur par .
Calculer la valeur exacte de .
Correction
Question 7
Déterminer .
Correction
Question 8
On admet que . Que peut-on en déduire graphiquement ?
Correction
Nous savons que
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
- Si alors la fonction admet une asymptote verticale d'équation
- Si alors la fonction admet une asymptote verticale d'équation
Question 9
Calculer .
Correction
est dérivable sur .
Il vient alors que :
équivaut successivement à :
équivaut successivement à :
Question 10
Etudiez les variations de sur .
Correction
Pour tout réel , on vérifie aisément que .
Le signe de dépend alors de .
Il en résulte donc que :
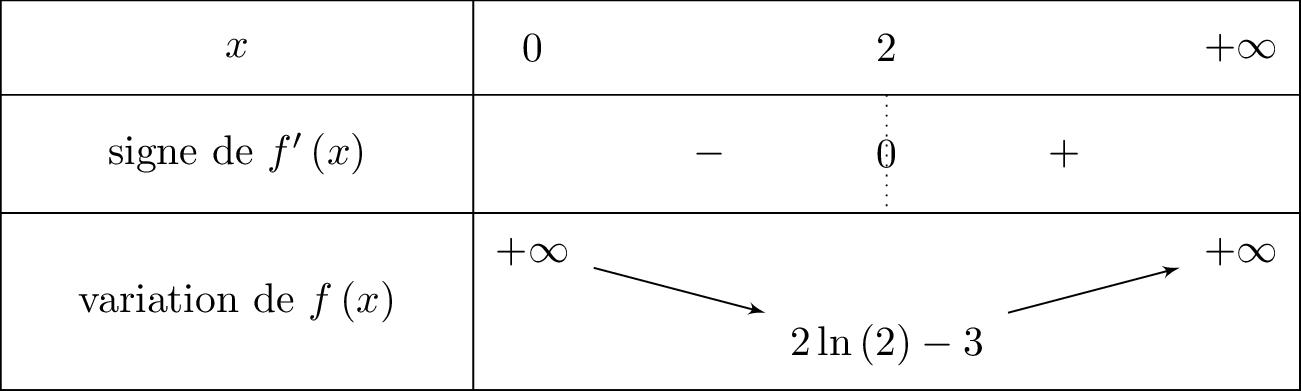
Le signe de dépend alors de .
Il en résulte donc que :
- si alors et donc est décroissante sur cet intervalle.
- si alors et donc est croissante sur cet intervalle.

Question 11
Soit la fonction définie et dérivable sur par .
Montrer que est une primitive de sur .
Correction
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que
Soit : Autrement dit, il faut que
On reconnaît la forme : avec ; et
Ainsi : ; et
Il vient alors que :
Ainsi :
Donc est bien une primitive de sur .
Question 12
Déterminer l’aire du domaine limité par la courbe , l’axe des abscisses et les droites d’équation et en unités d’aires. On donnera la valeur exacte puis une valeur approchée à près de .
Correction
Sur l’intervalle , est négative, donc l’aire du domaine limité par la courbe , l’axe des abscisses et les droites d’équation et est égale à :
Finalement :
Finalement :
unités d'aires.