Fonction logarithme népérien
Exercice 1 - Exercice 1
1 min
0
Un petit mélange Logarithme et Exponentielle.
Question 1
Soit la fonction définie sur par
Montrer que pout tout réel , on a : .
Correction
Pour tout réel , on a :
équivaut successivement à :
équivaut successivement à :
Question 2
Montrer que pour tout réel , on a : .
Correction
Pour tout réel , on a :
équivaut successivement à :
équivaut successivement à :
Question 3
Choisir la forme la mieux adaptée de pour déterminer :
La limite de en .
Correction
Nous allons utiliser la forme afin de déterminer la limite en .
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Autrement dit :
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Autrement dit :
Question 4
La limite de en . Que peut-on en déduire graphiquement?
Correction
Nous allons utiliser la forme afin de déterminer la limite en .
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Si alors la fonction admet une asymptote verticale d'équation
Si alors la fonction admet une asymptote verticale d'équation
Interprétation graphique : la courbe représentative de la courbe admet une asymptote verticale d'équation .Si alors la fonction admet une asymptote verticale d'équation
Question 5
la position de la courbe représentative de par rapport à la droite d’équation .
Correction
Il nous faut ici étudier le signe de .
Nous allons utiliser la forme
Il vient alors que :
équivaut successivement à :
Etudions maintenant le signe de .
équivaut successivement à :
.
Cela signifie donc que :
Nous allons utiliser la forme
Il vient alors que :
équivaut successivement à :
Etudions maintenant le signe de .
équivaut successivement à :
.
Cela signifie donc que :
- si , nous avons et donc . Cela se traduit par le fait que lorsque alors la courbe représentative de la courbe est situé en dessous de la droite d’équation .
- si , nous avons et donc . Cela se traduit par le fait que lorsque alors la courbe représentative de la courbe est situé au-dessus de la droite d’équation .
Question 6
la dérivée de et les variations de .
Correction
Nous allons utiliser la forme
est dérivable sur .
Pour tout réel , on vérifie aisément que et . En effet , car sinon ne serait pas définie.
Il en résulte donc que le signe de dépend de .
Comme , nous avons alors :
Il en résulte donc que pour tout réel , on a : et de ce fait la fonction est strictement croissante sur .
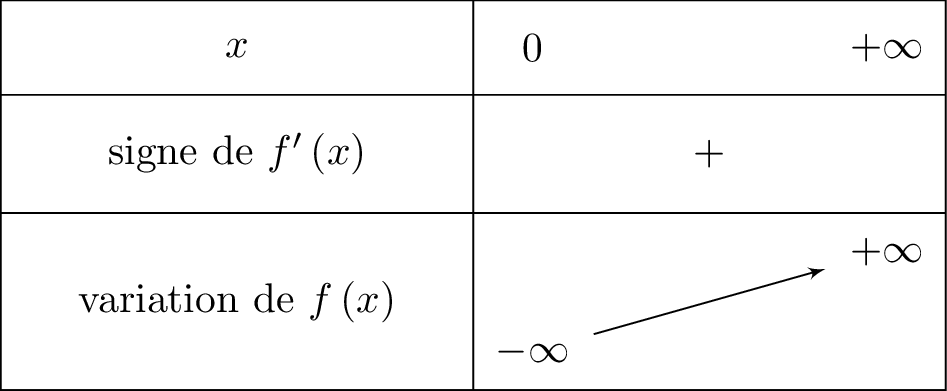
est dérivable sur .
Pour tout réel , on vérifie aisément que et . En effet , car sinon ne serait pas définie.
Il en résulte donc que le signe de dépend de .
Comme , nous avons alors :
Il en résulte donc que pour tout réel , on a : et de ce fait la fonction est strictement croissante sur .
