Vecteurs du plan : première Partie

Calculer les coordonnées du milieu d'un segment - Exercice 2

12 min
25
Soit (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) un repère orthonormé du plan. On considère les points A(6;−3)A\left(6;-3\right) et B(2;−1)B\left(2;-1 \right).
Question 1

Déterminer les coordonnées du point CC tel que BB soit le milieu de [CA]\left[CA\right].

Correction
Comme BB est le milieu de [CA]\left[CA\right], nous allons appliquer la méthode pour calculer les coordonnées d'un milieu.
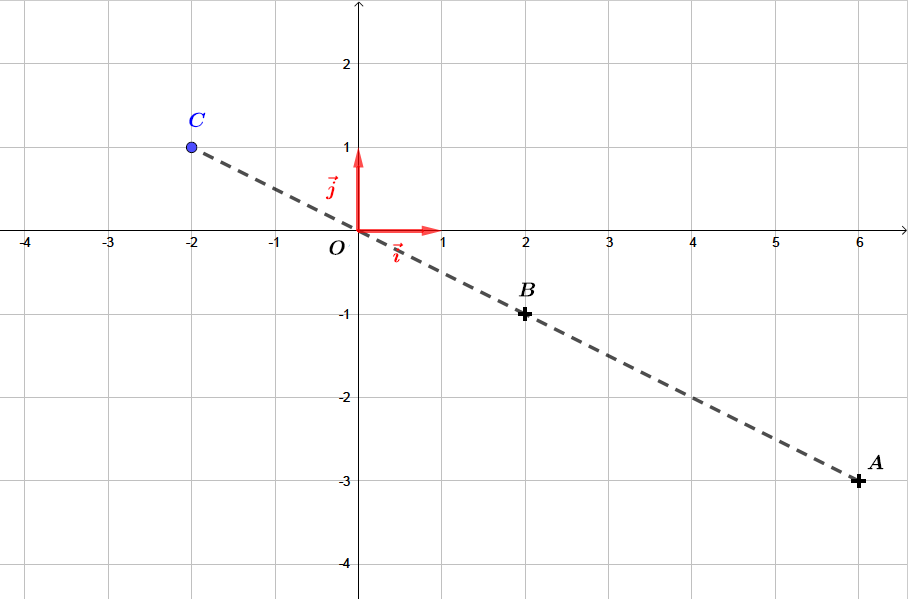
Soit (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) un repère orthonormé du plan et deux points A(xA;yA)A\left(x_{A} ;y_{A} \right) et B(xB;yB)B\left(x_{B} ;y_{B} \right)
  • Les coordonnées du milieu I(xI;yI)I\left(x_{I} ;y_{I} \right) du segment [AB]\left[AB\right] sont : xI=xA+xB2x_{I} =\frac{x_{A} +x_{B} }{2} et yI=yA+yB2y_{I} =\frac{y_{A} +y_{B} }{2}
Il vient alors que :
D’une part :\red{\text{D'une part :}}
xB=xA+xC2x_{B} =\frac{x_{A} +x_{C} }{2} équivaut successivement à :
2=6+xC22 =\frac{6+x_{C}}{2} . Ici, nous allons tout mettre au même dénominateur.
2×22=6+xC2\frac{2\times2}{2} =\frac{6+x_{C}}{2}
42=6+xC2\frac{4}{2} =\frac{6+x_{C}}{2}
  • A2=B2⇔A=B\frac{A}{2} =\frac{B}{2} \Leftrightarrow A=B
4=6+xC4=6+x_{C}
6+xC=46+x_{C}=4
xC=4−6x_{C}=4-6
xC=−2x_{C}=-2

D’autre part :\red{\text{D'autre part :}}
yB=yA+yC2y_{B} =\frac{y_{A} +y_{C} }{2} équivaut successivement à :
−1=−3+yC2-1 =\frac{-3+y_{C}}{2} . Ici, nous allons tout mettre au même dénominateur.
−1×22=−3+yC2\frac{-1\times2}{2} =\frac{-3+y_{C}}{2}
−22=−3+yC2\frac{-2}{2} =\frac{-3+y_{C}}{2}
  • A2=B2⇔A=B\frac{A}{2} =\frac{B}{2} \Leftrightarrow A=B
−2=−3+yC-2=-3+y_{C}
−3+yC=−2-3+y_{C}=-2
yC=−2+3y_{C}=-2+3
yC=1y_{C}=1

Les coordonnées du point CC tel que BB soit le milieu de [CA]\left[CA\right] sont C(−2;1)C\left(-2;1 \right)
Question 2
Soit (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) un repère orthonormé du plan. On considère les points C(−1;1)C\left(-1;1 \right) et D(−4;−1)D\left(-4;-1\right).

Déterminer les coordonnées du point EE tel que CC soit le milieu de [DE]\left[DE\right].

Correction
Comme CC est le milieu de [DE]\left[DE\right], nous allons appliquer la méthode pour calculer les coordonnées d'un milieu.
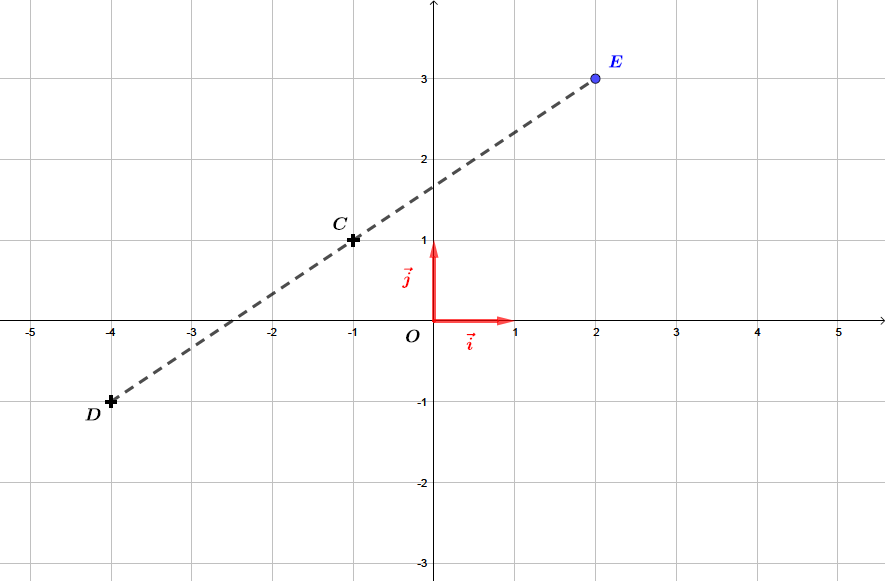
Soit (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) un repère orthonormé du plan et deux points A(xA;yA)A\left(x_{A} ;y_{A} \right) et B(xB;yB)B\left(x_{B} ;y_{B} \right)
  • Les coordonnées du milieu I(xI;yI)I\left(x_{I} ;y_{I} \right) du segment [AB]\left[AB\right] sont : xI=xA+xB2x_{I} =\frac{x_{A} +x_{B} }{2} et yI=yA+yB2y_{I} =\frac{y_{A} +y_{B} }{2}
Il vient alors que :
D’une part :\red{\text{D'une part :}}
xC=xD+xE2x_{C} =\frac{x_{D} +x_{E} }{2} équivaut successivement à :
−1=−4+xE2-1 =\frac{-4+x_{E}}{2} . Ici, nous allons tout mettre au même dénominateur.
−1×22=−4+xE2\frac{-1\times2}{2} =\frac{-4+x_{E}}{2}
−22=−4+xE2\frac{-2}{2} =\frac{-4+x_{E}}{2}
  • A2=B2⇔A=B\frac{A}{2} =\frac{B}{2} \Leftrightarrow A=B
−2=−4+xE-2=-4+x_{E}
−4+xE=−2-4+x_{E}=-2
xE=−2+4x_{E}=-2+4
xE=2x_{E}=2

D’autre part :\red{\text{D'autre part :}}
yC=yD+yE2y_{C} =\frac{y_{D} +y_{E} }{2} équivaut successivement à :
1=−1+yE21 =\frac{-1+y_{E}}{2} . Ici, nous allons tout mettre au même dénominateur.
1×22=−1+yE2\frac{1\times2}{2} =\frac{-1+y_{E}}{2}
22=−1+yE2\frac{2}{2} =\frac{-1+y_{E}}{2}
  • A2=B2⇔A=B\frac{A}{2} =\frac{B}{2} \Leftrightarrow A=B
2=−1+yE2=-1+y_{E}
−1+yE=2-1+y_{E}=2
yE=2+1y_{E}=2+1
yE=3y_{E}=3

Les coordonnées du point EE tel que CC soit le milieu de [DE]\left[DE\right] sont E(2;3)E\left(2;3 \right)

Question 3
Soit (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) un repère orthonormé du plan. On considère les points B(4;2)B\left(4;2 \right) et D(0;8)D\left(0;8\right).

Soit EE est le symétrique de DD par rapport à BB. Déterminer les coordonnées du point EE

Correction
EE est le symétrique de DD par rapport à BB signifie que le point BB est le milieu du segment [DE]\left[DE\right].
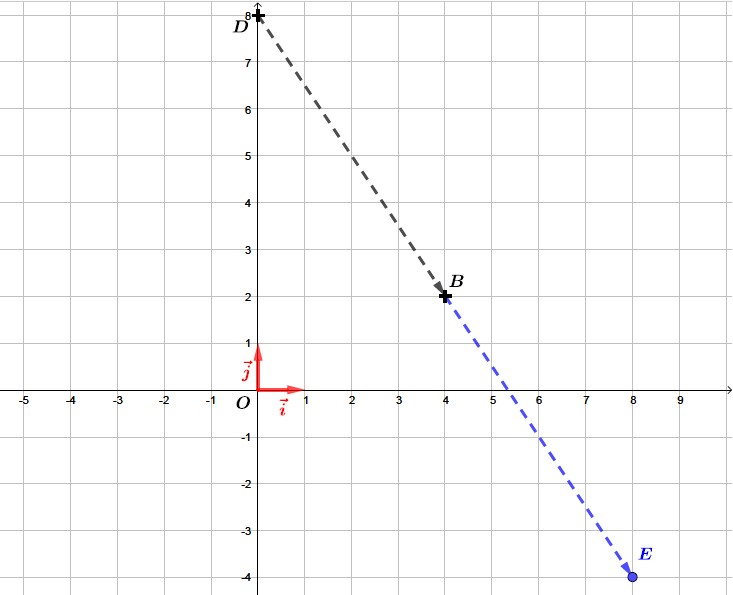
Soit (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) un repère orthonormé du plan et deux points A(xA;yA)A\left(x_{A} ;y_{A} \right) et B(xB;yB)B\left(x_{B} ;y_{B} \right)
  • Les coordonnées du milieu I(xI;yI)I\left(x_{I} ;y_{I} \right) du segment [AB]\left[AB\right] sont : xI=xA+xB2x_{I} =\frac{x_{A} +x_{B} }{2} et yI=yA+yB2y_{I} =\frac{y_{A} +y_{B} }{2}
Il vient alors que :
D’une part :\red{\text{D'une part :}}
xB=xD+xE2x_{B} =\frac{x_{D} +x_{E} }{2} équivaut successivement à :
4=0+xE24 =\frac{0+x_{E}}{2} . Ici, nous allons tout mettre au même dénominateur.
4×22=0+xE2\frac{4\times2}{2} =\frac{0+x_{E}}{2}
82=0+xE2\frac{8}{2} =\frac{0+x_{E}}{2}
  • A2=B2⇔A=B\frac{A}{2} =\frac{B}{2} \Leftrightarrow A=B
8=0+xE8=0+x_{E}
xE=8x_{E}=8

D’autre part :\red{\text{D'autre part :}}
yB=yD+yE2y_{B} =\frac{y_{D} +y_{E} }{2} équivaut successivement à :
2=8+yE22 =\frac{8+y_{E}}{2} . Ici, nous allons tout mettre au même dénominateur.
2×22=8+yE2\frac{2\times2}{2} =\frac{8+y_{E}}{2}
42=8+yE2\frac{4}{2} =\frac{8+y_{E}}{2}
  • A2=B2⇔A=B\frac{A}{2} =\frac{B}{2} \Leftrightarrow A=B
4=8+yE4=8+y_{E}
8+yE=48+y_{E}=4
yE=4−8y_{E}=4-8
yE=−4y_{E}=-4

Les coordonnées du point EE tel que BB soit le milieu de [DE]\left[DE\right] sont E(8;−4)E\left(8;-4 \right)